Inicio Discusiones Matemáticas discretas Probabilidad y Geometría (Elemental)
Discusiones
Temas
Probabilidad y Geometría (Elemental)
Analiza la relación entre geometría y probabilidad
Construir ruletas y hacer con ellas experimentos de probabilidad puede ser muy divertido aun para personas que pueden resolver problemas sin necesidad de actividades manuales. Con los CD (discos compactos) se pueden hacer buenas ruletas.
Mentor: En el juego que estudiaremos, los jugadores hacen una ruleta y se ponen de acuerdo en lo que ganarán si cae en su color. Por ejemplo:
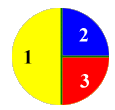
El jugador 1 gana 10 puntos si la ruleta se detiene en amarillo.
El jugador 2 gana 16 puntos si la ruleta se detiene en azul.
El jugador 3 gana 24 puntos si la ruleta se detiene en rojo.
¿Es un juego justo? ¿Cómo puede asegurarlo?
¿Cuáles son las probabilidades de que cada jugador gane puntos en un lanzamiento?
Estudiante 1: Los jugadores 2 y 3 tienen las mismas probabilidades de ganar. El jugador 1 tiene el doble de posibilidades.
Estudiante 2: El jugador 1 "posee" la mitad de la ruleta, y cada uno de los jugadores 2 y 3 "posee" un cuarto de la ruleta. Si queremos expresar en lenguaje matemático su probabilidad de ganar, podemos escribir:
P (jugador 1 gane) = 1/2 = .5 o 50%
P (jugador 2 gane) = 1/4 = .25 o 25%
P (jugador 3 gane) = 1/4 = .25 o 25%
Mentor: ¿Si el juego se repite muchas veces, cuál jugador esperas que gane más puntos?
Estudiante 1: Yo pienso que el jugador 2 ganará tantos juegos como el jugador 3, pero el jugador 3 obtiene más puntos cada vez...considero que el jugador 3 gana más puntos que el jugador 2,
Estudiante 2: Usemos "el truco de 100 experimentos" para comparar los jugadores con el jugador 1. En 100 experimentos, podemos esperar:
El jugador 1 gana 10 points 1/2 de 100 veces, o gana 10*1/2*100 = 500 puntos,
en promedio 10*1/2*100/100 = 10*1/2 = 5 puntos por lanzamiento.
El jugador 2 gana 16 points 1/4 de 100 veces, o gana 16*1/4*100 = 400 puntos,
en promedio 16*1/4*100/100 = 16*1/4 = 4 puntos por lanzamiento.
El jugador 3 gana 24 points 1/4 de 100 veces, en promedio 24*1/4 = 6 puntos por lanzamiento.
Estudiante 1: ¡Ahora puedo ver que el jugador 3 está mejor que los otros!
Mentor: ¿Puedes cambiar el número de puntos que obtiene cada jugador, para lograr un juego justo? Si el jugador 1 obtiene 4 puntos, ¿cuántos puntos deberían recibir los jugadores 2 y 3 para un juego justo? ¿Y si el jugador 1 recibe N puntos? Aquí N significa que no sabemos cuántos recibe exactamente. Lo que buscamos es establecer una conexión entre el número de puntos que obtiene el jugador 1 y el número de puntos que obtienen los jugadores 2 y 3.
Estudiante: Veamos...se espera que los jugadores 2 y 3 ganen cerca de la mitad de juegos que el jugador 1, y por lo tanto tendrían que obtener el doble de puntos cada vez que ganen. Esto significa 2*N cada uno.
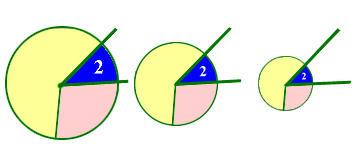
Mentor: Veamos una ruleta diferente; algo como esta:
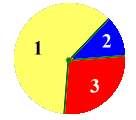
Estudiante 1:¿Cómo medimos ahora las probabilidades de cada jugador?
Estudiante 2: Sería buenísimo si pudiéramos medir con exactitud la "tajada" de cada jugador. ¿Cómo hacerlo?
Mentor: La gente mide las cosas comparándolas con unidades estándar. Puedes decir que una presentación dura 25 minutos, que un árbol tiene 12 metros de altura, que un perro pesa 23 kilogramos. Podemos usar ciertas unidades para medir la "tajada" o sector de la ruleta, para cada jugador. Antes de empezar, dime qué es diferente y qué el igual para estas tres ruletas.

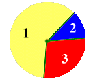
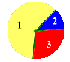
Esudiante 1: No importa cuál de las ruletas se usa para el juego. Las probabilidades de elegri cada color son las mismas
Estudiante 2: Los ángulos de cada color son iguales
Mentor: Tradicionalmente la gente mide ángulos en unidades especiales llamadas "grados" Estas unidades se escogieron de tal manera que el siguiente ángulo muy fácil de medir tenga 90 grados

Este ángulo se llama ángulo recto. Un tercio del ángulo recto tiene 30 grados, por ejemplo, etc. Hay una herramienta útil para medir ángulos, que se llama transportador Tiene unidades para grados, así como una regla tiene unidades para centímetros o pulgadas. Se puede medir un ángulo alineando la base del transportador con un lado del ángulo, poniéndolo de tal manera que el centro del transportador cae sobre el vértice del ángulo.
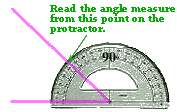 Lea la medida del ángulo en este punto sobre el transportador
Lea la medida del ángulo en este punto sobre el transportador
Estudiante 1: El ángulo del círculo completo tiene 360 grados, porque contiene cuatro ángulos rectos.
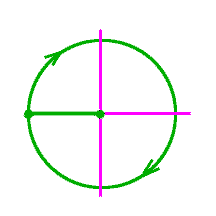
Estudiante 2: Esto significa que cada jugador tiene tantas probabilidades como su ángulo tiene de grados entre un total de 360 posiblilidades.
Mentor: ¿Qué ángulo te daría una probabilidad de ganar de 1/3?
Estudiante: Un tercio de 360 grados, es decir, 120 grados.
Mentor: Puedes construir varias ruletas para el juego y hallar, midiendo ángulos, las probabilidades exactas que cada jugador tiene de ganar. Escoge los puntos que ganará cada jugador de tal manera que el juego sea justo. Después juega muchas veces y mira si las probabilidades de ganancias reales son cercanas a tus predicciones.
De la probabilidad a la geometría
Mentor: En el juego de la ruleta visto antes usamos geometria (midiendo ángulos) para hallar la probabilidad de éxito de cada jugador. ¿Puedes dar otros ejemplos en los que podamos medir algo para hallar las probabilidades de obtener un determinado resultados?
Estudiante 1: Podemos medir áreas. Suponga que dejamos caer algo sobre una superficie y calculamos la probabilidad de que caiga en una parte específica de ella.
Estudiante 2: Sí; por ejemplo, ¿cuál es la probabilidad de que un meteorito que impacte la Tierra caiga en el agua? Necesitamos conocer el área de la Tierra y el área total de los océanos, mares, lagos y ríos, para responder la pregunta.
Mentor: ¿Se te ocurre un ejemplo con volúmenes?
Student 1: OK.Estamos trabajando en una mina de oro. Tenemos un lota de arena regular mezclada con arena con oro. ¿Cuál es la probabilidad de que un grano que escojamos es de oro? Tenemos que medir el volumen de oro en la arena para encontrar la respuesta.
Estudiante 2: Pero, para hacer eso se necesita sacar todo el oro. Después de hacerlo, ¿a quién le importan las probabilidades? La arena ya no estará mezclada y ¡nadie la mezclará solamente para repetir el experimento!
Mentor: ¿Podría ser que el gerente, quien tiene que decidir si se justifica refinar el siguiente lote de arena, se interese en las probabilidades? Tu pregunta conduce inmediatamente al tema de cómo las probabilidades pueden usarse para responder preguntas sobre medidas geométricas. Piensa que quieres medir cuánto oro hay en tu lote de arena. Para hacerlo con exactitud tendrías que extraer todo el oro. ¿Y si no se justifica? ¿Qué harías?
Estudiante: Llenaría unos cuantos baldes con arena y hallaría exactamente qué tanto oro hay en ellos.Si un tercio de la arena de los baldes es oro, entonces aproximadamente un tercio de la arena es también oro.
Mentor: Así que tomarías arena aleatoriamente y encontrarías la probabilidad de hallar oro en ella. Veamos si la probabilidad puede ayudarnos a medir los ángulos de las ruletas. Si no tienes un transportador, ¿cómo puedes usar la probabilidad para estimar los ángulos amarillo, azul y rojo en esta ruleta?

Estudiante: Puedo girar la ruleta muchas veces y registrar en qué color cae cada vez. Si resulta el amarillo 65% de las veces, entonces el ángulo amarillo es aproximadamente 65% del círculo es decir, 360*.65 = 234 grados.
Mentor: ¿Será una medida exacta, o una estimación?
Estudiante: Una estimación.
