Inicio Discusiones Matemáticas discretas Probabilidad y Resultado
Discusiones
Temas
Probabilidad y Resultado
Mentor: Veamos a varias personas participando en juegos sencillos de azar. El Jugador 1 lanza un dado de seis caras y gana si sale un 2 o un 3 y pierde en cualquier otro caso. El Jugador 2 lanza un dado de 4 caras y gana si obtiene un 1. ¿Qué chances de ganar tiene cada jugador?
Estudiante: Podemos decir que el primer jugador gana en dos de seis casos posibles.
Mentor: Los científicos también usan la palabra resultado en lugar de la palabra "caso". Cada resultado es una descripción completa de una situación que puede presentarse como resultado de un experimento (exactamente la información importante). En nuestro juego, el número mostrado tras el lanzamiento del dado es todo lo que nos interesa: no nos importa que tanto rueda el dado, qué tan lejos cae del jugador, etc. ¿Qué jugador tiene un mejor chance de ganar y por qué?
Estudiante: El Jugador 1 ganará con más frecuencia porque gana en dos casos y el Jugador 2 solamente en un caso.
Mentor: ¿Así es? Déjame presentarte al Jugador 3, que usa una gran ruleta con números de 1 a 100 y gana si la ruleta se detiene en 96,97,98, 99 o 100. De los tres jugadores, ¿cuál gana con más frecuencia y por qué?
Estudiante: El Jugador 3 gana en cinco casos. Esto es más que lo de los otros dos jugadores, pero ahora hay un centenar de resultados...!Así que contar resultados no es suficiente!
Mentor: Pensemos por un momento en un problema distinto. Esto te ayudará a aclarar algunas cosas. Supongamos que tenemos nuevamente tres jugadores, sólo que ahora en un juego diferente.Cada uno tiene una larga caja rectangular de la misma longitud y anchura, un balón y un mono. Cada mono lanza de cualquier manera un balón en la caja de cada jugador, de modo que cae en una posición aleatoria dentro de la caja. Los fondos de las cajas están divididos en partes iguales por medio de líneas delgadas. Las secciones están pintadas de colores claros y oscuros, como se ve en el dibujo siguiente. La caja del Jugador 1 está dividida en 6 partes, 2 de ellas oscuras; la caja del Jugador 2 está dividida en 4 partes, una de ellas oscura; y la caja del jugador 3 está dividida en 100 partes, cinco de ellas oscuras. Si el balón cae en la parte oscura de la caja, el jugador gana. ¿Cuál jugador tiene mejores posibilidades de ganar?
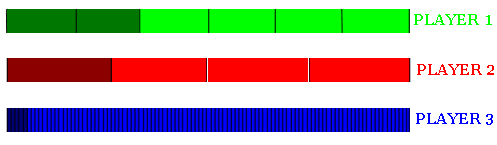
Estudiante: Si las cajas tienen igual longitud y anchura, entonces el Jugador 1 tiene la mayor posibilidad de ganar porque su porción ganadora es la más grande.
Mentor: ¿Qué tiene que ver este juego con el primero?
Estudiante: El Jugador 1 gana en 2 de 6 resultados posibles, y el Jugador 2 en 1 de 4 posibles. Pero en el segundo juego cada resultado del Jugador 1 se ve menor que cada resultado del Jugador 2, y los resultados del Jugador 3 son todavía menores. ¡Son minúsculos! En el primer juego no sabemos qué tan "grandes" son los resultados. ¿O sí?
Mentor: Esta es una gran pregunta. Pensemos en todos los posibles resultados para el Jugador 1 en el primer juego, es decir, los números 1,2,3,4,5 o 6 del dado de seis caras. Ahora pensemos en todos los resultados para el Jugador 2, es decir, los números 1, 2, 3 o 4 del dado de cuatro caras, y los resultados para el Jugador 3, esto es, todos los números desde 1 hasta 100 de la ruleta. Si cada jugador ganara sin importar qué número obtuvo con el dado o con la ruleta, ganaría con igual frecuencia que cualquier otro jugador ¡siempre! Esto nos dice que conjuntamente todos los posibles resultados para cada jugador (por jemplo, los números desde 1 hasta 100 para el Jugador 3) conllevan la misma cantidad de "suerte" que todos los posibles resultados de cualquier otro jugador: toda la suerte que se puede tener, 100% de suerte y no una parte o fracción de ella.
Estudiante: ¡Entonces, tiene sentido mirar al "gran total " como a una caja que tiene la misma longitud para cada jugador, aunque un número diferente de "compartimientos"!. No importa cómo escoja los números cada jugador, el significado es el mismo. Ahora entiendo cómo cinco resultados ganadores para el Jugador 3 representan un chance mucho menor que un resultado ganador para el Jugador 2!
Mentor: Podemos hacer dibujos para comparar los chances de ganar. Sin embargo es algo tedioso; los dibujos no nos dan más infomación que los números, sólo nos ayudan a que la información tenga más sentido. Hay maneras de dar sentido a los números sin necesidad de las gráficas. Para hacerlo, podemos expresar en diferentes formas el chance o la probabilidad que cada jugador tiene de ganar. En lugar de decir "El primer jugador gana en dos de seis resultados", podemos decir: "El primer jugador gana en dos-sextos (o un-tercio, que es lo mismo) de los resultados", o "La probabilidad de ganar del primer jugador es 1/3". Y, dado que 1/3=0.33 (redondeado a dos dígitos después del punto decimal), podemos decir: " La probabilidad de ganar del primer jugador es .33". Si miras el dibujo nuevamente, puedes ver que el área oscura para el Jugador 1 es realmente un tercio del total.

Estudiante: Entonces la probabilidad de ganar para el Jugador 2 es .25.
Mentor: Hay todavía otra forma de expresar probabilidades. Si algo pasa siempre, ello significa que sucede en el 100% de todos los casos. Y si algo pasa la mitad del tiempo, sucede en 1/2 del 100% de todos los casos, o 1/2*100%=50% de los casos. Y si algo pasa en 1/3 de todos los casos (esa es la probabilidad de ganar del Jugador 1), podemos decir: "La probabilidad de ganar del primer jugador es 1/3 de 100%, o 1/3 *100%=33.33%" redondeado a dos dígitos después del punto."
Estudiante: Entonces la probabilidad de ganar del Jugador 3 es 5%
Mentor: Hagamos ahora un experimento. Supongamos que eres el Jugador 1. Juega el juego muchas veces (100-200) utilizando un dado o un programa de computador y registra el número de veces en que ganas (es decir, el número de veces en que sacas un 2 o un 3). Después de cada juego, anota la razón acumulada de veces en que ganaste a número de jugadas hasta ese momento, llamada probabilidad experimental, en fracciones y en decimales. Es conveniente usar una tabla en la que se registran estas dos cantidades: el número total de juegos efectuados y el número total de juegos ganados.
Probabilidad experimental de ganar:
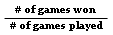
# juegos ganados
# juegos jugados
Probabilidad experimental de ganar (en porcentaje)

# juegos ganados * 100%
# juegos jugados
Estudiante: En un comienzo las razones cambian muchísimo con cada juego. Después de muchos juegos cambian menos y menos Yo usé un computador para simular 1000 juegos, y las razones se mantuvieron casi iguales con cada nuevo juego. Estuvieron muy cercanas a .33 o 33%.
Mentor: ¿Cuál crees que es la razón para que la probabilidad experimental se acerque a la probabilidad teórica?
