Inicio Actividades Números y operaciones Generador de cristales
Generador de cristales
Temas
Generador de cristales
¿En qué consiste la actividad Generador de cristales ?
Esta actividad permite que el usuario construya sus propios fractales por deformación de una recta.
Los fractales por deformación de una recta son ejemplos interesantes de un proceso repetitivo. Aquí comenzamos con una recta y la doblamos en una serie de segmentos conectados. Uno puede generar fractales regulares e irregulares de esta manera.
Veamos un ejemplo de un fractal regular. La recta será dividida en cuatro segmentos iguales y doblada así:

Ahora se presenta el proceso repetitivo: al continuar al siguiente paso, cada segmento de recta individual es remplazado por una copia a escala de la deformación original:

Repita esta proceso una y otra vez. A medida que el número de pasos tiende al infinito, nace un fractal. Como nuestros ojos no pueden distinguir segmentos muy pequeños, usualmente podremos tener una buena idea de cómo será el fractal, después de unos 5 pasos:

También podemos desarrollar fractales irregulares dividiendo la recta original en segmentos desiguales. Veamos:

Un paso más adelante:

Cinco pasos más adelante:

Recursos para la clase
Actividad
¿Cómo puedo utilizar esta actividad?
Descripción
Esta actividad permite que el usuario construya sus propios fractales por deformación de una recta.
Controles y Resultados
- El Área para dibujar , en la parte superior del “simulación”, es la región en la que se dibuja el fractal.
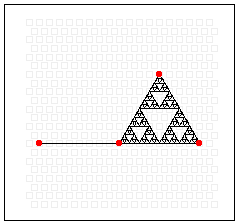
Usted puede definir manualmente cómo será dibujado el fractal, moviendo los puntos rojos sobre la pantalla. A medida que mueve los puntos rojos, el “simulación” le va mostrando cómo será el fractal. Sin embargo, si usted incrementa el número de pasos para que el dibujo del fractal requiera más tiempo, la imagen obtenida cuando mueve los puntos será apenas una versión simplificada del fractal que se dibujará cuando libere el punto rojo.
- Los botones Bajar uno o Subir uno controlan cuántos pasos del fractal serán dibujados. Usted también puede seleccionar el número de pasos en el menú desplegable que aparece entre tales botones.
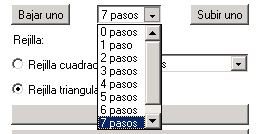
- Usted puede escoger entre dos clases de rejillas: Rejilla cuadrada o Rejilla triangular . La diferencia entre ellas es la región para situar los puntos rojos: En la cuadrada, los puntos se disponen en un cuadrado, y en la segunda en un triángulo. En consecuencia, es mejor utilizar la rejilla cuadrada cuando se van a dibujar figuras de tipo cuadrado, y la rejilla triangular cuando se van a dibujar triángulos.

- En la celda Puntos usted selecciona el número de puntos rojos que quiere que aparezcan en el dibujo.
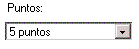
- El botón Reiniciar coloca todos los puntos en el centro del área y borra el fractal en el que usted estaba trabajando, para que pueda empezar uno nuevo.
- Esta versión de El fabricante de cristales es algo limitada. Usted puede ensayar una Versión completa haciendo clic en el botón de Ir a la versión completa.
Recursos y contexto curricular
Esta actividad permite al usuario generar interesantes fractales irregulares. Si usted utiliza las preguntas de exploraciónesta actividad funcionará bien con 2 o 3 estudiantes y les tomará unos 25 o 30 minutos; de lo contrario, requerirá unos 15 minutos.
Ubicación en el currículo de matemáticas
Esta actividad se puede utilizar para:
- Practicar la habilidad de los estudiantes para reconocer patrones.
- Practicar con las habilidades de los estudiantes en geometría plana.
- Ilustrar las ideas de auto similaridad y recursión.
- Experimentar con objetos fractales.
Estándares alcanzados
Esta actividad se puede usar para referirse a los siguientes estándares:
- Estándares de geometría
- Analizar características y propiedades de formas geométricas de dos y tres dimensiones, y desarrollar argumentos matemáticos acerca de relaciones geométricas.
- Aplicar transformaciones y usar simetría para analizar situaciones matemáticas.
Esté preparado para:
- Dar a los alumnos instrucciones implícitas sobre lo que deben hacer. Por ejemplo “Hoy vamos a descubrir cómo hacer fractales utilizando....”
- Discutir sobre fracciones y simetría
