Estudiante: Yo sé cómo graficar funciones lineales, pero me confundo al graficar desigualdades.
¿Cuáles son las diferencias entre graficar funciones lineales y graficar desigualdades? 

Mentor: Bueno, hay varias diferencias. Una desigualdad lineal es muy parecida a una función lineal si es menor que, menor que o igual, mayor que, o mayor que o igual a un número,
Entonces, no hay un valor de y que corresponda a un solo valor de x; más bien hay muchos valores posibles de y correspondientes a un sólo valor de x, que satisfacen la desigualdad,

Estudiante: ¿Cómo encontramos los valores de x y de y?

Mentor: Consideremos la desigualdad  2x+3y < 9. ¿Qué podríamos hacer para encontrar los valores máximos de x y de y en esta desigualdad?

Estudiante: Bueno, como el valor de 2x+3y es menor que 9, los valores máximos de x y de y se presentan cuando este valor es 9.

Mentor: ¡Correcto! Entonces, grafiquemos la recta máxima de esta desigualdad encontrando la gráfica de la recta si x y y fueran lo más grandes posible. En otras palabras, grafiquemos la recta como si la función fuera 2x+3y = 9.

Estudiante: Esa es una función lineal y yo sé cómo graficarla. Primero despejo y de tal manera que obtengo una función de la forma y=mx+b. Dejaré y en un lado, así que la función es           3y = -2x + 9  y despejo y dividiendo ambos lados por 3. La ecuación final es y=-2/3x + 3.

Mentor: Ahora, ¿por qué es útil poner la función en esa forma?

Estudiante: ¡Porque me muestra la pendiente y el intercepto en y! La pendiente es el número antes de la x, que me dice que tan empinada es la recta y el número mismo me dice dónde intersecta la línea al eje y.

Mentor: De acuerdo. Entonces la pendiente de la recta es -2/3 y el intercepto en y es 3. Veamos esa recta en una gráfica, usando la aplicación desigualdad
 

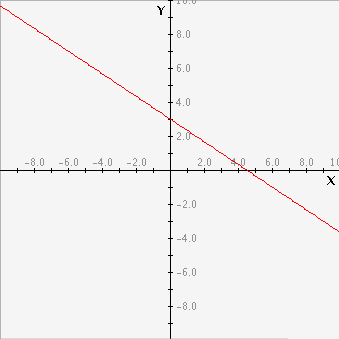
Estudiante: ¡Puedo ver que la recta cruza el eje y exactamente en 3! Además, la pendiente se ve como la pendiente real (-2/3) porque por cada dos unidades que disminuye el valor de y, hay un aumento de 3 unidades en la dirección positiva del eje x. ¡Esta es la gráfica de la función 2x+3y = 9! Pero lo que queremos es graficar la desigualdad 2x+3y < 9. Entonces, ¿qué hacemos ahora? 

Mentor: Puesto que se trata de una desigualdad, hay muchos valores de x y y que la satisfacen Por ejemplo, los que satisfacen la función 2x+3y = 8 o la función  2x+3y = 2.

Estudiante: O  2x+3y = -10 o  2x+3y = 0.05.

Mentor: ¡Exactamente! Hay una cantidad interminable de funciones inmersas en esta desigualdad. En lugar de graficar cada posible función (lo cual sería una tarea imposible) sombreamos toda el área situada por debajo de la recta 2x+3y=9. El sombreado mostrará que todas las funciones por debajo de esta recta satisfacen la desigualdad. Las funciones que hemos mencionado, 2x+3y=8, 2x+3y=2, 2x+3y=-10 y  2x+3y=0.05 (al igual que muchas otras)
 existen en el área sombreada de la gráfica. Veámoslo: 

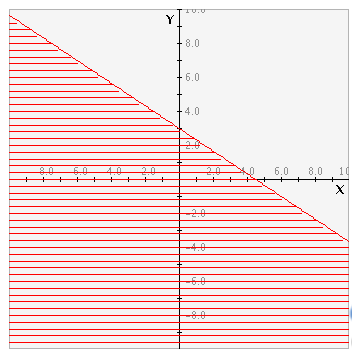
Estudiante: ¡Uao!, Entonces cada función lineal que quede sobre esa recta o por debajo de ella es parte de la función 2x+3y < 9.

Estudiante: Ok, entonces esto significa que si se hubiera tratado de 2x+3y >= 9, toda el área sobre la recta 2x+3y=9 se habría sombreado?

Mentor: ¡Así es exactamente! Si 2x+3y >= 9, entonces 2x+3y podría tomar valores como 10, 20.7, y aún 1,000. Todas aquellas funciones estarían sobre la recta 2x+3y=9 en una gráfica. Aquí se ve una  gráfica de 2x+3y >= 9:

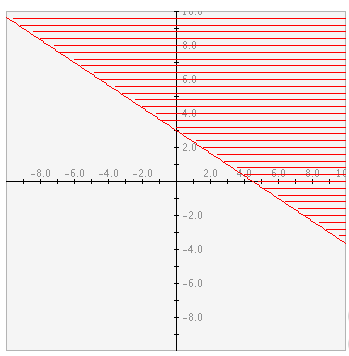
Estudiante: ¡Ok. Esto tiene sentido!  ¿Y si la función fuera 2x+3y>9? En este caso la función 2x+3y no es igual a 9. En consecuencia la función  2x+3y=9 no podría ser parte de la gráfica. ¿Cómo se graficaría? 

Mentor:

¡Buena pregunta! En realidad, todavía graficaríamos la recta 2x+3y=9, pero en lugar de hacerlo con una linea sólida, usamos una linea punteada, para comunicar la idea de que 2x+3y=9 no satisface la función 2x+3y>9, pero que sí la satisface cualquier valor sobre recta. Así se vería: 

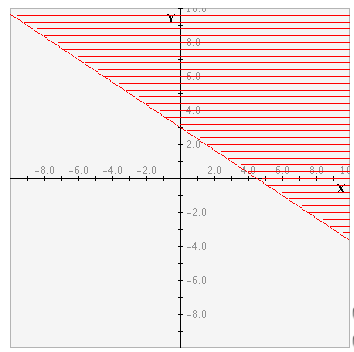
Estudiante: Esta gráfica es muy parecida a la de 2x+3y >= 9. De verdad que no puedo ver la línea punteada. 

Mentor: Como esta gráfica es muy grande, no puedes ver mucho detalle. Si configuraras la ventana en un área más pequeña, podrías ver mejor la línea discontinua. Ahora, sabiendo que cuando tengas la desigualdad 2x+3y > 9 usarías una línea punteada y sombreado sobre la recta 2x+3y=9, ¿qué se te ocurre que  harías en el caso de la desigualdad 2x+3y < 9?

Estudiante: Usaría una línea discontinua para graficar  2x+3y=9 ya que la función 2x+3y es menor que, pero no igual a 9. Además, sombrearía por debajo de esa línea punteada porque es una desigualdad menor que. 

Mentor: ¡Excelente trabajo! Estás listo para experimentar con la actividad Desigualdades