Inicio Actividades Funciones y conceptos del álgebra Bomba de funciones de dos variables
Bomba de funciones de dos variables
Temas
Bomba de funciones de dos variables
¿En qué consiste la actividad Bomba de funciones de dos variables ?
Esta actividad permite al usuario seguir los pasos para graficar una función de dos variables y juzgar si un punto inicial de partida es un prisionero o un fugitivo, para entender los números complejos y los sistemas de Julia.
Para entender El conjunto de Julia y finalmente el conjunto de Mandelbrot, el fractal más famoso del mundo, debemos ser capaces de calcular y graficar funciones cuadráticas de números complejos. La forma mas fácil de visualizar los números complejos es entenderlos como pares ordenados. Las funciones de estos números se pueden describir, en la forma usual, como “máquinas de entradas y resultados”, solo que entra un par ordenado y sale un par ordenado.

Las Operaciones Básicas para esta nueva situación son:
| Suma de dos pares (+) |
Componentes- i.e., (a,b) + (c,d) = (a+c,b+d) |
|
Resta de dos pares (-) |
Componentes- i.e., (a,b) - (c,d) = (a-c,b-d) |
|
Multiplicación por un número (*) |
Componentes- i.e., x * (a,b) = (x*a,x*b) |
|
División por un número (/) |
Componentes- i.e., (a,b) / x = (a/x,b/x) |
|
Elevar al cuadrado un número (^2) |
(a,b) ^2 = (a^2 - b^2, 2ab) |
Un ejemplo de esta función es: f (Z) = Z^2 + (1/2,1/2). Estamos interesados en encontrar un punto de partida, colocándolo en la función para obtener un nuevo punto y luego volverlo a colocar en la función para obtener otro punto nuevo, y así sucesivamente. Por ejemplo podemos empezar con el punto (0,0) y colocarlo en la función:
f(0,0) = (0,0)^2 + (1/2,1/2) = (0,0) + (1/2,1/2) = (.5,.5)
f(.5,.5) = (.5,.5)^2 + (.5,.5) = (0,.5) + (.5,.5) = (.5,1)
f(.5,1) = (.5,1)^2 + (.5,.5) = (-.75,1) + (.5,.5) = (-.25,1.5)
f(-.75,1.5) = (-.75,1.5)^2 + (.5,.5) = (-2.1875,-.75) + (.5,.5) = (-1.6875,-.25)
f(-1.6875,-.25) = (-1.6875,-.25)^2 + (.5,.5) = (2.7852,.84375) + (.5,.5) = (3.2852,1.34375)
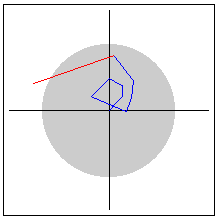
Aquí tenemos el gráfico:

Parece que los puntos saltaran por todos lados, alejándose del punto (0,0) y dejando finalmente el círculo gris de radio 2. Podemos ensayar otros puntos de partida y ver qué sucede en cada situación. Hay tres cosas que pueden suceder: Los Puntos pueden:
-
Acercarse más y más a 0 – decimos que tienden a 0. Estos son los prisioneros.
-
Volverse más y más grandes – decimos que tienden a infinito. Estos son los fugitivos. Sabemos que son fugitivos si están a más de dos unidades de su origen.
-
Quedar atrapados – estos puntos se encuentran en el límite entre los prisioneros y los fugitivos. El conjunto de todos estos puntos para una función se llama el Conjunto de Julia.
Los Conjuntos de Julia son las bases para la construcción del conjunto de Mandelbrot. Podemos encontrar los conjuntos de Julia mirando los límites entre prisioneros y fugitivos.
Recursos para la clase
Actividad
¿Cómo puedo utilizar esta actividad?
Descripción
Esta actividad permite al usuario seguir los pasos para graficar una función de dos variables y juzgar si un punto inicial de partida es un prisionero o un fugitivo, para entender los números complejos y los sistemas de Julia.
Controles y Resultados
-
Estas cajas, ubicadas en la parte de abajo del “simulación”, es donde usted debe entrar un Punto de partida y una Constante, C, para la función cuadrática f(Z) = Z^2 + C que usted quiere iterar.

-
Cuando quiera cambiar el Punto de partida o la Constante, haga clic en el botón Reiniciar para obtener un nuevo gráfico con esos valores. Luego haga clic en el botón Siguiente paso para calcular la siguiente iteración.
-
El Gráfico muestra la trayectoria (también llamada órbita) del punto de partida cuando se ingresa a la función. La línea roja es la trayectoria desde el punto anterior hasta el ultimo punto. Si la trayectoria de la orbita se sale del círculo gris de radio 2, se garantiza que el punto de partida es un fugitivo.
El Listado de la izquierda es otra forma de ver los valores de la función—como pares ordenados.
Recursos y contexto curricular
Esta actividad permite al usuario seguir los pasos para graficar una función de dos variables y juzgar si un punto inicial de partida es un prisionero o un fugitivo, para entender los números complejos y los conjuntos de Julia. Si usted utiliza las preguntas de exploración esta actividad funcionará bien con grupos de 3 a 5 estudiantes y les tomará unos 45 minutos o de lo contrario, requerirá unos 20 minutos.
Ubicación en el currículo de matemáticas
Esta actividad se puede usar para:
- Practicar las habilidades aritméticas.
- Practicar las habilidades de graficación.
- Introducir a los estudiantes a los números complejos.
- Motivar las nociones de conjuntos de Julia, prisioneros y fugitivos.
Estándares alcanzados
Esta actividad se usar para referirse a los siguientes estándares:
- Estándar de números y operaciones
- Entender los números, forma de representarlos, relaciones entre ellos y sistemas de números.
- Estándar de álgebra
- Entender patrones, relaciones y funciones.
Esté preparado para:
-
Dar instrucciones sobre lo que deben hacer los estudiantes. Por ejemplo “Hoy vamos a aprender sobre prisioneros, fugitivos y números complejos, usando la actividad “Bomba de funciones de dos variables” y su hoja de trabajo…”
-
Responder a la pregunta “¿Qué es un prisionero y un fugitivo?”
-
Discutir sobre números complejos y cómo graficarlos.
