Inicio Actividades Matemáticas discretas El peine de Cantor
El peine de Cantor
Temas
El peine de Cantor
¿En qué consiste la actividad El peine de Cantor ?
Esta actividad permite al usuario involucrarse en la construcción de un peine de Cantor.
El Peine de Cantor es una manera de visualizar el famoso Conjunto de Cantor. Comience con un segmento de recta así:

Ahora remueva el tercio central del segmento:

Luego remueva los tercios centrales de cada uno de los segmentos que se tienen. El paso siguiente sería:

Ahora repita este proceso indefinidamente. El Peine de Cantor es lo que queda después de remover los tercios centrales de los segmentos "un número infinito de veces."
Otros peines de Cantor se pueden crear removiendo partes centrales de diferentes tamaños. Por ejemplo, podemos remover el cuarto de la mitad (1/4) ó la mitad central (½) para así tener diferentes Peines de Cantor. Para distinguir entre ellos, a veces llamamos la versión original “El Peine de Cantor de tercios-medios”, utilizando un nombre similar para los otros peines.
Georg Cantor (1845-1918) se interesó mucho en conjuntos infinitos, especialmente en aquellos con propiedades inusuales. Él construyó lo que ahora se denomina el Conjunto de Cantor para ilustrar un conjunto infinito inusual. En este conjunto quedan únicamente puntos, no segmentos de recta, y en consecuencia no hay longitud. Si usted suspende el proceso en una etapa cualquiera, ahí hay segmentos de recta, aunque muy cortos. La idea es que en cualquier etapa usted tiene longitud, pero en el limite no. Esto hace que el Peine de Cantor sea un conjunto muy curioso.
Recursos para la clase
Actividad
¿Cómo puedo utilizar esta actividad?
Descripción
Esta actividad permite al usuario participar en el proceso de construcción de un Peine de Cantor.
Controles y Resultados
- El área rectangular en la parte superior del “simulación” muestra el fractal, que consiste en un conjunto de segmentos de color rojo.
- Los botones Paso anterior y Siguiente paso lo adelantarán o retrocederán un paso en el proceso de dibujar.

- Esta celda indica la longitud de los segmentos rojos que forman el fractal (como una fracción de la longitud total) y en cuál paso de la iteración del fractal está usted
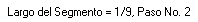
- En la celda marcada como Fracción eliminada, digite la fracción de cada segmento de la recta que desea remover en cada paso. Digite el numerador en la primera celda y el denominador en la segunda celda. 1/3 es el valor asignado por defecto. Dé clic en el botón Enviar para iniciar con un nuevo valor para la Fracción Eliminada

Recursos y contexto curricular
Esta actividad permite al usuario participar en el proceso de construcción de un Peine de Cantor. Está indicada para grupos de 2 o 3 estudiantes de habilidad mixta, por períodos de 30 a 45 minutos si se utilizan las preguntas de exploración, y por 10 minutos en caso contrario.
Ubicación en el currículo de matemáticas
Esta actividad se puede usar para:
- Practicar las habilidades de los estudiantes en el manejo de las fracciones.
- Practicar la habilidad de los estudiantes en encontrar o determinar patrones.
- Mostrar la complejidad del infinito.
- Motivar las ideas de auto-similaridad y recursión.
- Presentar objetos fractales.
- Motivar la idea de límite.
Estándares alcanzados
- Entender números, maneras de representarlos, relaciones entre ellos y sistemas numéricos.
- Entender el significado de las operaciones y cómo ellas se relacionan entre si.
- Calcular correctamente y hacer estimaciones razonables.
- Entender patrones, relaciones y funciones.
- Aplicar técnicas, herramientas y formulas apropiadas para determinar medidas.
Esté preparado para:
- Trabajar en la primera tabla de preguntas de exploración con los estudiantes.
- Discutir los conceptos de infinito y de límite.
- Revisar la multiplicación de fracciones.
