Inicio Actividades Estadística Distribución sesgada
Distribución sesgada
Temas
Distribución sesgada
¿En qué consiste la actividad Distribución sesgada ?
Esta actividad permite al usuario experimentar el movimiento de la mediana lejos del promedio en una distribución continua.
Distribuciones continuas como la normal y la lognormal, así como otras distribuciones como la exponencial que no se muestran aquí, ocurren en la medida en que el número de ensayos tiende a infinito. Esto quiere decir que si usted mide por años, una y otra vez, la altura de las plantas en un cultivo de trigo, el histograma que se obtiene se parecerá más y más a una curva suave.
Casi siempre que se miden eventos naturales se obtiene una distribución normal. El promedio, la mediana y la moda ocasionalmente pueden ser diferentes, especialmente cuando se trabaja con conjuntos pequeños de datos. Si se trabaja con conjuntos grandes de datos, obtenidos de eventos naturales, la distribución es normal; sin embargo ocurre a veces que con conjuntos grandes de datos el promedio, la mediana y la moda son diferentes.
Cuando el promedio, la mediana y la moda son diferentes, se obtiene algo llamado “distribución sesgada”. Este “simulación” le permite explorar diferentes distribuciones sesgadas para familiarizarse con su configuración.
Si usted mide el tiempo que toma a sus estudiantes dar una vuelta completa a una pista de carreras, o si pesa muchos objetos, o si mide la altura de varias plantas, o cualquier otra medición que dé como resultado números positivos, usted verá una distribución sesgada. En el caso de las vueltas alredor de la pista, probablemente a una persona promedio le tome digamos tres minutos. Algunos serán más rápidos, pero a otros les tomará cinco minutos o más, que a aquellos que lo hagan en un minuto, o en menos. Puede ser que a alguien le tome siete minutos, pero nadie podrá hacerlo en -1 minuto. Por lo tanto la distribución de la curva no será simétrica. En vez de que alguien pueda terminar la carrera en dos minutos menos o en dos minutos más que el promedio, podría ser que lo lograra en la mitad, o en el doble del tiempo promedio. Igualmente, si usted graficara las notas de sus alumnos, nadie podría superar el puntaje máximo posible (100%), pero podría haber varios estudiantes que obtuvieran calificaciones cercanas al máximo posible, y pocos, o muy pocos, que sacaran notas bajas.
Notas sobre la distribución Lognormal para el maestro
La curva normal tiene una forma única, aun cuando puede ser más alta y delgada, o más baja y gruesa, o se puede mover hacia la izquierda o hacia la derecha del eje x. A diferencia de la distribución normal, la distribución Lognormal es considerada como una familia de distribuciones y no una figura única con parámetros variables. Esta distribución puede tener muchas variaciones en su forma y también se puede sesgar. Existen muchas distribuciones sesgadas de muchas familias que tienen la misma mediana y desviación estándar. Decidimos escoger la distribución Lognormal porque se asemeja visualmente a la distribución normal, es fácil de manipular en el computador y con frecuencia se usa en análisis de datos similares a aquellos en los cuales se utilizaría una curva normal. La curva que grafica este “simulación” es tan solo una de muchas posibilidades.
La distribución Lognormal tiene valores positivos solamente, y la protuberancia se encuentra siempre en la parte inferior. Cada valor de la diferencia entre la mediana y la media (de hecho, el valor que se acepta de ‘mediana’) tiene asociado un promedio, una mediana y un sesgo cuando se asocia con una desviación estándar – sin tener realmente mayor ‘libertad’ que la curva normal, porque el cambio de forma está directamente ligado al cambio de ubicación en el gráfico. Si la mediana se encuentra por encima del promedio, se logra la apariencia de sesgo negativo y este cambio hace que la curva se posicione en el lugar correcto (con el promedio en cero). Lo que hice fue NO hacer una representación exacta de la curva Lognormal, sino mostrar un tipo de distribución que podría presentarse en una situación real, donde un factor componente estuviera afectando una variable de distribución normal. Esto puede parecer trivial y un asunto puramente matemático, pero quise adherirme a la ciencia, donde estas cosas son posibles, y no simples matemáticas.
Recursos para la clase
Actividad
¿Cómo puedo utilizar esta actividad?
Descripción
Esta actividad le permite al usuario experimentar mover la mediana del promedio en una distribución continua.
Controles y Resultados
- El Gráfico muestra una distribución normal. El promedio está dibujado con una línea azul, la mediana con una línea azul clara y la desviación estándar con una línea roja en cualquier lado del promedio. Los círculos negros en la parte inferior de las líneas rojas, y la línea azul clara, se pueden arrastrar con el ratón para cambiar la desviación estándar y la mediana. Note que la línea azul no se podrá ver si la línea azul clara es trasladada al mismo sitio. El pequeño gráfico rojo en la esquina superior izquierda muestra la escala de la cuadrícula.
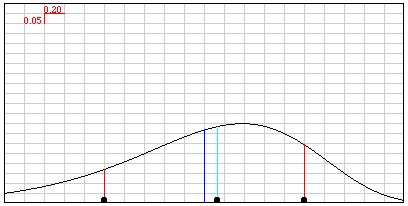
- Usted también puede generar una nueva desviación estándar escribiendo este valor en el cuadro Nueva desviación estándar y haciendo clic en el botón Fijar. La desviación estándar actual aparece en un letrero debajo del gráfico. La mediana se puede cambiar siguiendo el mismo procedimiento en el cuadro Nueva mediana.
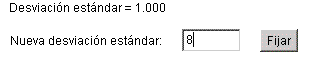
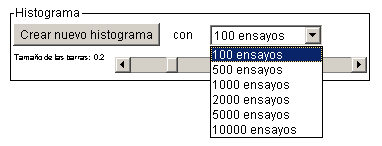
- Para dibujar un histograma, escoja el número de ensayos en el menú desplegable y haga clic en el botón Crear nuevo histograma. Usted puede cambiar el tamaño de las barras usando la barra de desplazamiento.
Recursos y contexto curricular
Esta actividad permite al usuario experimentar con distribuciones continuas, o de múltiples ensayos, donde el promedio, la mediana y la moda no son iguales. Esta actividad está indicada para grupos de dos a cuatro personas, y les tomará de 20 a 25 minutos si se utilizan las preguntas de exploración, y de 5 a l0 minutos, en caso contrario.
Ubicación en el currículo de matemáticas
Esta actividad se puede usar para:
-
Reforzar gráficamente los conceptos de mediana y desviación estándar.
-
Demostrar la diferencia entre datos teóricos (número infinito de ensayos) y datos reales (muestra pequeña o grande)
Estándares alcanzados
Esta actividad está orientada hacia el logro de los siguientes estándares:
- Análisis de datos y probabilidad
-
Hacer preguntas que se puedan formular con datos, y recolectar, organizar, y presentar datos relevantes para responderlas.
-
Seleccionar y usar métodos estadísticos apropiados para analizar datos.
-
Esté preparado para:
-
Responder a la pregunta: “¿Qué hace que una distribución sea sesgada?”
-
Discutir el tamaño de la muestra y sus efectos en el resultado de un experimento.
