Inicio Actividades Cálculo La ruleta ajustable
La ruleta ajustable
Temas
La ruleta ajustable
¿En qué consiste la actividad La ruleta ajustable ?
Esta actividad permite al usuario explorar la probabilidad teórica y experimental cambiando el área de las secciones coloreadas del círculo. Cuando se añade una sección el “simulación” reduce las otras secciones en forma proporcional. Cuando esto sucede, la probabilidad de que la aguja caiga en el mismo color cambiará.
La probabilidad teórica es la probabilidad basada en el tamaño de la sección comparada con todo el círculo. Si hay dos secciones iguales, se podría esperar que al hacer dos giros, la aguja caerá una vez en cada una de las secciones. La probabilidad experimental es el resultado real después de hacer el experimento un número dado de veces.
Pascal inició el estudio de probabilidad a principios del siglo XVII. Un buen día alguien le hizo una pregunta sobre el juego. Ésta fue: “Si dispongo de ocho lanzamientos para sacar un seis y en los tres primeros no lo logro, ¿cuánto me deben devolver de la apuesta si me retiro en eso momento?” El juego involucraba el azar, como la mayoría de los juegos hoy en día, por ejemplo el Monopolio y el juego de cartas. Las Vegas es una cuidad que está dominada por gente que ha invertido mucho en esta rama de las matemáticas. En la actualidad, el uso de la probabilidad se ha extendido a los campos de la ciencia, la medicina y la estadística.
Recursos para la clase
Actividad
¿Cómo puedo utilizar esta actividad?
Descripción
Esta actividad permite al usuario explorar la probabilidad teórica y experimental cambiando el área de las secciones coloreadas en el círculo.
Controles y Resultados
- Para cambiar el ancho de una sección, arrastre los puntos negros (pero no el punto blanco de referencia) en los límites de la sección:
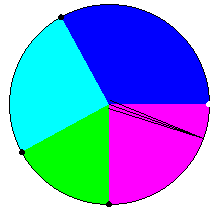
- También se puede cambiar el número de secciones manipulado las barras deslizadoras, o utilizando los campos de entrada a la derecha. Una vez que haya hecho el cambio, dé clic en el botón Actualizar.
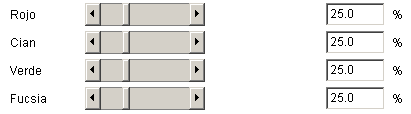
- Para aumentar el número de secciones en 1, haga clic en el botón +1 que está al lado del texto Número de secciones [___]. Para disminuir el número de secciones en 1, haga clic en el botón -1. Fíjese en el número de secciones en el espacio Número de secciones. En este caso tenemos 4.

- Para simular girar la ruleta, haga clic en el botón Girar:

- Cada vez que haga clic en Girar, usted puede cambiar el número de giros simulados, digitando el número en el espacio ¿Cuántos giros? [___]. En este caso tenemos 1.

- El programa le dice en que sección está la aguja. (La aguja esté en la sección azul/ fucsia/etc.), así como el número de veces que la aguja ha girado (Número de giros hasta el momento).
- El cuadro en la parte de abajo del programa le muestra La probabilidad experimental, La probabilidad teóricay los Totales (el número de veces que la aguja ha caído en esa sección), para cada una de las secciones.
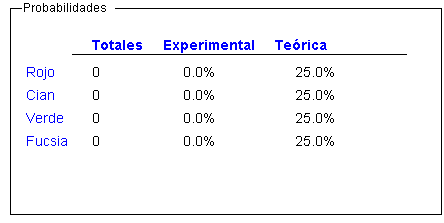
- Al hacer clic en botón de la casilla Mostrar cuadro de resultados, aparece una ventana externa que muestra los resultados experimentales en formato de gráfico de torta.

- Usted puede borrar todos los datos experimentales y empezar con un nuevo giro, iniciándolo en cero, haciendo clic en la casilla Nuevo experimento.

- Para cambiar el color de una sección, simplemente haga clic en ella. Aparecerá enseguida un menú desplegable que le permitirá escoger un color de una lista. Luego de clic en Sí para completar el cambio.
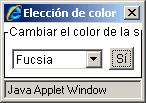
Recursos y contexto curricular
Esta actividad permite al usuario explorar la probabilidad teórica y experimental cambiando el área de las secciones coloreadas en el círculo. Esta actividad está indicada para grupos de dos personas, y les tomará de 15 a 20 minutos si se utilizan las preguntas de exploración, y l0 minutos, en caso contrario.
Ubicación en el currículo de matemáticas
Esta actividad se puede usar para:
-
Introducir las nociones de azar y probabilidad.
-
Mostrar la diferencia entre probabilidad experimental y teórica.
-
Motivar la relación entre probabilidad y geometría.
Estándares alcanzados
-
-
Analizar características y propiedades de figuras geométricas bidimensionales y tridimensionales y desarrollar argumentos matemáticos sobre relaciones geométricas.
-
-
-
Entender los atributos medibles de los objetos y las unidades, sistemas y procesos de medición.
-
Aplicar las técnicas, herramientas y formulas apropiadas para determinar la medición.
-
-
Análisis de datos y probabilidad
-
Entender y aplicar conceptos básicos de probabilidades.
-
Esté preparado para:
-
Dar instrucciones claras sobre lo que van a hacer en el día de hoy. Por ejemplo: “Hoy vamos a experimentar con el “simulación” La ruleta y veremos cómo si se varía el área de las secciones se afecta las posibilidades de caer en .….”
-
Responder la pregunta: “¿Cómo puedo aprender a medir en grados?”.
-
Discutir la geometría de los círculos.
