Coordenadas polares

El sistema de coordenadas polares es una forma de graficar un punto en dos dimensiones, en forma similar al sistema de coordenadas cartesianas. Se basa en un punto central llamado el polo (el origen en el sistema cartesiano)  y un eje que se extiende en dirección positiva desde el polo, llamado eje polar (el eje x en el sistema cartesiano). Cada punto se define mediante un par ordenado (r, theta) en el que r es la distancia desde el polo y theta es el ángulo entre el eje polar y el segmento de recta entre el punto y el polo. 

Este es un ejemplo: 

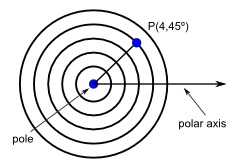
polo                                         eje polar 

Aunque las funciones algebraicas tradicionales se pueden graficar en un sistema de coordenadas polares, es con las funciones trigonométricas que los resultados son particularmente interesantes.

Las coordenadas polares se utilizan intensivamente en navegación. También para modelar sistemas que presentan simetría radial como el flujo de agua subterránea o fuerza radial como los campos gravitacionales.   

Descripción

Esta actividad permite al usuario graficar pares ordenados y funciones algebraicas o trigonométricas en el mismo plano de coordenadas polares.

Controles y Resultados

• La gráfica se muestra en la parte superior de la pantalla.

  

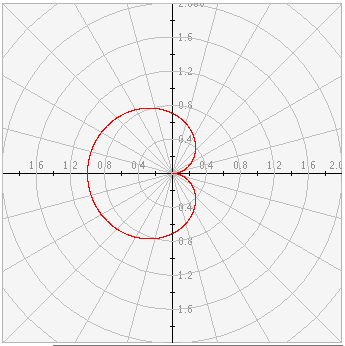
• Las funciones se ingresan en el área Función. Para graficar una función, digite la fórmula en el espacio anexo al texto "f(t)=" que queda en la parte inferior de la aplicación; t representa "theta". Se pueden graficar hasta 10 funciones en el mismo diagrama. Para graficar varias funciones ingrese las fórmulas en lineas
  separadas, así: 
    
  Las funciones básicas y sus composiciones se pueden escribir así: 

• Función	Símbolo	Ejemplos	Significado
  suma	+	x + 3	x más tres
  resta	-	5 - x	cinco menos x
  multiplicacion	*	x*(x - 2)	x por la cantidad x menos 2
  división	/	3/x	tres dividido por x
  potencia	^	x^3	x elevado a la tres
  (pi)	pi	sin(pi*x)	seno de la cantidad (pi) por x
  raíz cuadrada	sqrt(...)	sqrt(x)	raíz cuadrada de x
  raíz n-sima*	x^(1/n)	x^(1/3)	raíz cúbica de x
  valor absoluto	abs(...)	abs(3 - x)	valor absoluto de la cantidad tres menos x
  e a la potencia x	exp(...)	exp(x)	e a la potencia x
  seno	sin(...)	sin(x)	seno de x
  coseno	cos(...)	cos(5 - x)	coseno de la cantidad cinco menos x
  tangente	tan(...)	tan(x)	tangente de x
  arcoseno	asin(...)	2*asin(x)	dos por arcoseno de x
  arcocoseno	acos(...)	acos(x)	arcocoseno de x
  arcotangente	atan(...)	atan(x)	arcotangente of x
  seno hiperbólico	senh(...)	sinh(x)	seno hiperbólico de x
  coseno hiperbólico	cosh(...)	cosh(10/x)	coseno hiperbólico de la cantidad diez dividido entre x
  tangente hiperbólica	tanh(...)	tanh(x)	tangente hiperbólica de x
  logaritmos natural	ln(...)	ln(x)	logaritmo natural de x
  logartitmo en base 10	log(...)	log(x + 5)	logaritmo en base 10 de la cantidad x más 5

  NOTA:  Si para una función dada hay un rango de valores en los que la función no está definida, esta aplicación dibujará una línea recta sobre el rango no definido. 

• Los puntos se ingresan en el área Datos. Estos puntos deben estar en la forma     (r, theta). Se requiere un espacio o un "enter"  para separar los datos de un punto de los de otro. Después de ingresar las coordenadas, debe presionar el botón Graficar/Actualizar, para graficarlos.

• 

  Si tiene dificultades copiando los datos de la aplicación y pegándolos en una hoja de Excel, consulte nuestra Ayuda Copy/Paste de Excel
  
  Si se escoge la opción Usar Radianes, los valores para theta pueden ingresarse usando la palabra pi, como en pi/4 o 2pi/3. También puede usar las funciones de    la lista anterior para crear los valores de r. 

  Si los valores de r o de theta son negativos es necesario convertirlos en valores equivalentes y positivos apropiados. Si el valor de theta es mayor que 2 pi, se lo debe convertir a un valor apropiado menor o igual a 2 pi. 

• Así como se pueden graficar hasta 10 funciones a la vez, se pueden graficar hasta 12 conjuntos de datos a la vez.  Para separar conjuntos de datos múltiples escriba newgraph en una misma línea en la ventana de Datos. Si prefiere especificar colores propios para las gráficas, puede remplazar newgraph con las siguientes palabras: bluegraph(azul), redgraph (rojo)  greengraph (verde), graygraph (gris) magentagraph (magenta), orangegraph (naranja), purplegraph (violeta), crimsongraph (carmesí), blackgraph (negro), browngraph (café), darkbluegraph (azul oscuro)
• 
  Usted puede elegir qué desea ver en la gráfica. Por ejemplo, que muestre todas las funciones, todos los datos y/o las líneas de cuadrícula, seleccionando las casillas de verificación o los botones en la casilla Mostrar
   
• La aplicación también puede indicar en qué punto se produce cada click. Haga click en el ratón en cualquier punto del gráfico y aparecerán las coordenadas del punto en la casilla Posicióin del ratón
   
• Incremento automático. Seleccionando la casilla Incremento Automático se obtiene la ventana más pequeña posible en la que caben en el plano coordenado  todos los puntos. (Nota: Debe haber datos para que esta caracteristica funcione), También puede elegir grados o radianes para los datos. Si elige grados, el valor de t será dado en grados cuando se muestre la tabla de datos.
• 
• Los valores Mínimo Theta y Máximo Theta permiten que el usuario ajuste el rango de la función. 

• Mostrar radio permite que el usuario ajuste manualmente el tamaño de la ventana de visualización. También puede utilizar el "zoom" con este propósito. Dado que las coordenadas polares se definen por la distancia desde el polo y el ángulo con el eje polar, la ventana de visualización siempre será un cuadrado con el polo en su centro.  
  

• Para ver una tabla de valores correspondiente a la función graficada, presione el botón  (Mostrar tabla de datos).
   

• Los valores de t se incrementan uniformemente y producen los correspondientes valores f(t) para cada función graficada. Esos valores se pueden cambiar definiendo nuevos valores máximo y mínimo para theta y para el tamaño del incremento, expresado todo en radianes. Si define un incremento que no divide exactamente el rango, la tabla se detendrá en el mayor múltiplo del incremento que sea menor que el máximo. El campo Precisión permite ajustar el número de cifras decimales que se muestran.

    

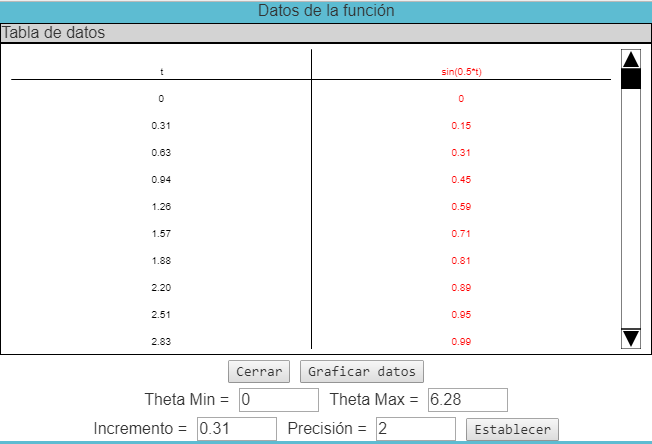
• Cuando se presiona el botón Graficar datos  de la ventana Mostrar tabla de datos, los datos de la tabla se representan en la pantalla principal
  Gráfica de sin(.5*t) in rojo y de sin(2t) in azul: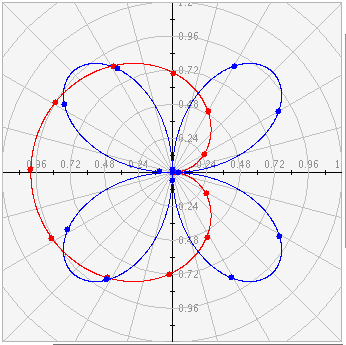

  

  Adicionalmente a la gráfica de la pantalla principal, en el área de texto se muestran los datos correspondientes a los puntos representados.

  

Esta actividad permite al usuario graficar pares ordenados y funciones algebraicas o trigonométricas en el plano de coordenadas polares. La actividad es apropiada para trabajarse en grupos de dos a cuatro estudiantes durante unos cuarenta y cinco minutos si se utilizan las preguntas de exploración  y durante unos veinte minutos en caso contrario.    

Esta actividad puede usarse para:

• hacer una introducción al sistema de coordenadas polares
• que los estudiantes pongan en práctica sus habilidades para graficar puntos
• mostrar la conversión entre grados y radianes

Grado 10

• Funciones y relaciones
  • El estudiante demuestra comprensión conceptual de funciones, patrones y sucesiones, incluidas las que se presentan en situaciones del mundo real.
  • El estudiante demuestra pensamiento algebraico

Grado 9

• Funciones y relaciones
  • El estudiante demuestra comprensión conceptual de funciones, patrones y sucesiones, incluidas las que se presentan en situaciones del mundo real.
  • El estudiante demuestra pensamiento algebraico

• explicar la diferencia entre coordenadas cartesianas y coordenadas polares
• explicar la diferencia entre radianes y grados
• explicar funciones periódicas

• Discusión sobre Graficar funciones en el sistema de coordenadas polares
• Discusión sobre Coordenadas polares
• Lección sobre Coordenadas polares
• Taller Preguntas de exploración sobre coordenadas polares 
• Taller Preguntas de exploración sobre coordenadas polares (doc)