Estudiante: Yo entiendo los conceptos relacionados con secciones cónicas, pero ¿Cómo puedo graficarlos algebraicamente? ¿Hay ecuaciones que deban memorizarse?

Mentor: Es cierto que puedes memorizar las ecuaciones, pero son bien complicadas y las cuatro son tan parecidas que es fácil confundirse. Te aseguro que te irá mucho mejor si deduces tú mismo las ecuaciones.

Estudiante: Sería muy bueno comprender lo que hay  en el fondo de estas ecuaciones. Así, si las olvido en alguna prueba, las puedo deducir sin problema.

Mentor: ¡Exactamente! Comencemos con la más simple de estas ecuaciones, la circunferencia.  ¿Cuál es la definición geométrica de circunferencia? (no la definición como sección cónica). 

Estudiante: Una circunferencia son todos los puntos que están a una cierta distancia, r, de un punto dado. 

Mentor: De acuerdo. Podrías decir, entonces, que la distancia de cualquier punto al centro es siempre la misma. ¿Podrías usar el Teorema de Pitágoras para calcular esa distancia? 

Estudiante: Bueno, podríamos trazar rectas desde su centro hasta un punto sobre  la circunferencia y calcular su longitud, formando a partir de ellas triángulos rectángulos, así: 

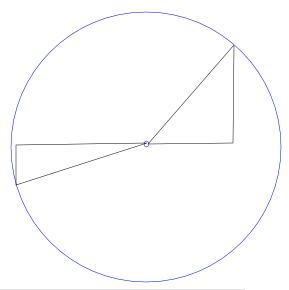
Mentor: ¡Muy bien!  Ahora, si decimos que el centro de la circunferencia está en un punto (h, k) y que (x, y) es el punto sobre la circunferencia, ¿podrias encontrar una ecuación para el radio r? 

Estudiante: Bueno, primero tendríamos que encontrar la longitud de cada lado. La longitud del lado horizontal sería la diferencia en los valores de x entre el centro y el punto sobre la circunferencia, es decir, x - h. Igualmente, la longitud del lado vertical sería la diferencia en los valores de y, es decir, y - k. 

Mentor: ¡Bien! ¿Cuál es, entonces, la longitud del radio?

Estudiante: La longitud del radio es  r² = a² + b², por lo tanto, sería:

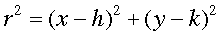
Mentor: ¡Precisamente!  Ahora, ¿qué pasa si usamos un punto diferente sobre la circunferencia?

Estudiante: Obviamente, x and y serían diferentes, pero el centro del círculo, (h, k), y el radio r son los mismos.  Entonces, ¿la ecuación no sería la misma que la del primer punto?

Mentor: ¡Claro que sí!  Tu ecuación es, de hecho, la ecuación general de la circunferencia de centro el punto (h, k) y radio r

Estudiante: ¡Uao! ¿Las ecuaciones de las otras tres secciones cónicas también se determinan a partir de sus definiciones geométricas? 

Mentor: Si; en efecto, así fue como se llegó a las ecuaciones originalmente. Veámoslo en el caso de la elipse. Pero antes, reescribamos la ecuación de la circunferencia dividiendo ambos lados por r²:

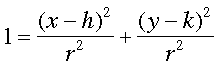
Mentor: Ahora, si miramos la gráfica de esta circunferencia, ¿puedes decirme cuánto mide el eje horizontal, en términos del radio r?  

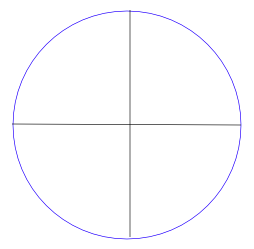
Estudiante: Naturalmente, es igual al diámetro, que es 2r. 

Mentor: Bien. ¿Puedes ahora justificar tu respuesta algebraicamente?

Estudiante: Bueno, si   y = k, entonces la ecuación se reduce a:

---> 

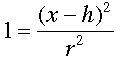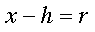
Mentor: ¡Oh-oh! Creo que olvidaste algo sobre sacar raiz cuadrada...

Estudiante:¡Ah, sí! Tengo que incluir

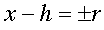
Mentor: Sí, en este caso el doble signo es particularmente importante, porque los dos puntos están sobre la circunferencia. 

Estudiante: Correcto, porque entonces la distancia entre los dos puntos es   r - (- r) = 2 r, que es la longitud del eje horizontal. 

Mentor: ¡Bien! Ahora, ¿puedes encontrar la longitud del eje vertical algebraicamente? 

Estudiante: Seguro. Cuando  x = h, la ecuación se reduce a :

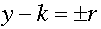
Estudiante:  Lo cual da como resultado una longitud de 2 r, lo mismo que el eje horizontal. 

Mentor: ¡Absolutamente correcto!  En una circunferencia todos los diámetros son iguales, asi que tanto x - h como  y - k están divididos por r², donde 2 r es la longitud de cualquiera de los ejes.  Pero, ¿ y qué sucede cuando se trata de una elipse?

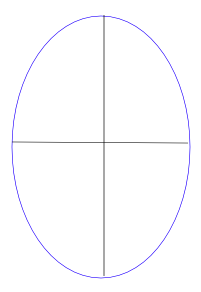
Estudiante: Humm,  una elipse es básicamente una circunferencia,  sólo que uno de los ejes es más largo que el otro.  Asi que en lugar de dividir los dos términos en  x y y por  r², tal vez podriamos dividirlos por a² y b², con lo cual tendriamos  2 a para el eje horizontal y 2 b para el eje vertical. 

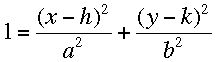
Mentor: ¡Exacto!  Entonces si y = k, tendríamos x - h = ±a, y si  x = h, tendríamos y - k = ±b.

Mentor: Ahora, consideremos una hipérbola. Aun cuando su gráfica se ve muy diferente de la del círculo o la elipse, apuesto a que puedes encontrar la ecuación a partir de la definición geométrica.  

Estudiante: Bueno, dado que una hipérbola se define como todos los puntos tales que la diferencia entre sus distancias a dos focos es la misma, es básicamente una elipse volteada de adentro hacia afuera.   

Mentor: Correcto. En efecto, si graficas una elipse y una hiperbola en la misma gráfica (con las mismas constantes) obtienes algo como esto:

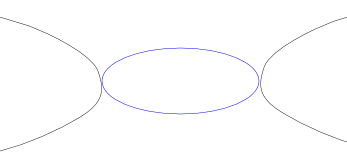
Estudiante: En tal caso, creo que la ecuación sería precisamente así:

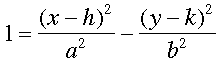
o

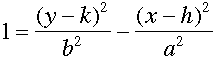
Mentor: ¡Precisamente! Me gusta mucho que hayas recordado que la sustracción puede ir en ambos lados. En efecto, esas ecuaciones definen, respectivamente,  una hipérbola que se abre horizontalmente y una hipérbola que se abre verticalmente,  

Estudiante: Si; eso tiene sentido. ¿Y con respecto a una parábola? ¿Se relaciona con las otras?

Mentor: Sí; geométricamente una parábola se define como un conjunto de puntos equidistantes de un foco y de una directriz. Entonces, usando nuevamente el Teorema de Pitágoras, si el vértice de la parábola está en el punto (h, k) esta ecuación parece razonable: 

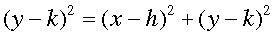
Mentor: ¿Puedes ver si esta ecuación funciona?

Estudiante: Bueno, la ecuación se puede simplificar

 ---> -->

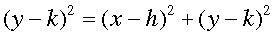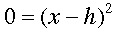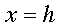
Estudiante: ¡Espere un momento! Esto no puede ser cierto; esa es la ecuación de una recta vertical. 

Mentor: Ciertamente, esto no es correcto. ¿Qué puede estar mal en mi ecuación original 

Estudiante: Me parece que el  (y - k)² de la izquierda no es el mismo (y - k)²  de la derecha. 

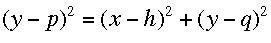
Mentor:¡Bien pensado! La directriz y el foco no están a la misma distancia vertical desde cada punto, por lo tanto, no deben tener el mismo término en la ecuación. Ahora que tenemos la ecuación correcta, ¿cómo podemos resolver esta ecuación para y? 

Estudiante:  Parece que debemos desarrollar los binomios en y para despejar y  después

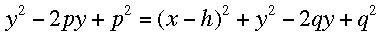
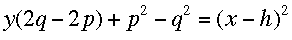
Mentor: ¡Bien! Ahora despejamos  y, con lo cual obtenemos: 

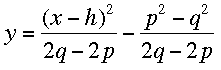
¡Pero esta ecuación es demasiado complicada! ¿Cómo podemos simplificarla un poco?

Estudiante: Humm...Yo no veo cómo simplificar el término con x puesto que tenemos cuatro variables diferentes, pero el otro término se puede factorizar para obtener: 

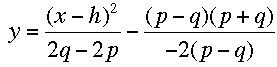
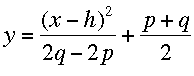
Mentor: ¡Exacto! Ahora, si hacemos  x = h, ¿qué obtenemos? Recuerda que la distancia desde cualquier punto de la parábola hasta el foco y la directriz es la misma.  

Estudiante:  Como la x- distancia  is cero, la y- distancia al foco y a la directriz debe ser la misma. Entonces,  y es la semisuma de p con q, esto es, y es el punto medio entre el foco y la directriz. En consecuencia, ¡y debe ser el vértice de la paráabola!

Mentor: Sí; realmente, así es: La coordenada y del vértice es precisamente la semisuma o promedio de los valores de y para el foco y la directriz. 

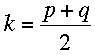
Estudiante: Qué bien! Entonces, ¿qué podemos hacer con la otra parte de la ecuación?

Mentor: Si suponemos que el vértice de la parábola está en (0,0), ¿puedes simplificar la ecuación?  

Estudiante:  Bueno, para que el vértice sea el punto medio entre el foco y la directriz necesitamos que  p = - q. Por lo tanto, la ecuación es

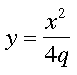
Mentor: ¡Exacto! En cualquier parábola, q es la distancia desde el foco o la directriz hasta el vértice. ¿Qué pasaría si el centro estuviera en (h, k) en lugar de (0, 0)? 

Estudiante:  Humm, puesto que sólo estamos desplazando la gráfica, la distancia foco/directriz hasta el vértice debería seguir siendo la misma. Por lo tanto la ecuación debería ser

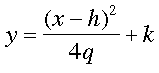
Mentor: Exactamente; ahora tienes la ecuación general de la parábola.