Estudiante: Entonces, ¿qué representa la r?

Mentor: La r representa la fuerza del coeficiente de correlación  R puede estar entre +1 y -1. Para visualizar este concepto podemos graficar los puntos  (1,2), (2,3) y (3,4) en la actividad   Regresión. ¿Qué observas?

Estudiante:  Hay una línea recta ascendente, y dice r=1.

Mentor: Sí. Esto significa que hay una correlación positiva muy fuerte entre los datos. ¿Qué relación consideras que debe existir entre los valores de x y de y para que haya una correlación positiva?

Estudiante: Bueno, en este caso cuando X crece también crece Y. Yo pienso que si cuando una variable se hace más grande también se hace más grande la otra, entonces hay una correlación positiva. 

Mentor: ¡Es correcto!  Una recta horizontal tiene r=0. Esto significa que no hay relación entre las dos variables y los valores de Y están dispersos aleatoriamente en la cuadrícula. ¿Puedes adivinar cómo sería la recta cuando r=-1? Trata de responder, experimentando con el diagrama de dispersión.

Estudiante: Si r=-1 entonces la recta tendrá una correlación negativa y creo que apuntará sostenidamente hacia abajo. 

Mentor: Así es. Ahora, si añades el punto aislado (9,3) al diagrama de {(1,5) (2,4) (3,3) and (4,2)} (que tiene un  r-valor de -1) ¿qué crees que le pasará a la recta de mejor ajuste? ¿Cuál crees que será el valor de r?  Puedes utilizar la actividad Regresión. como ayuda para visualizar esto.

Estudiante: Creo que la recta tendrá un ajuste hacia arriba en dirección del punto aislado y por lo tanto no irá consistentemente hacia abajo. Esto significa que la correlación no será tan fuertemente negativa y se alejará de -1 hacia +1. Sin embargo, todavía tendrá una inclinación hacia abajo. ¿Tal vez r=-.4? 

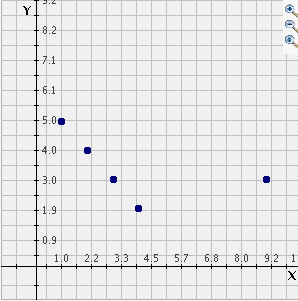
Mentor: Bueno, pues seleccionemos la Recta de mejor ajuste y veamos 

Estudiante: Hey! No estaba tan lejos. 

Mentor: Cierto. En este caso r=-.54, pero estás en la ruta correcta.  Sólo recuerda que la recta de mejor ajuste debe dar cuenta del punto aislado junto con el resto de los datos,  y por eso no es fácli  predecirla.  Puedes utilizar este programa para explorar la correlación de diferentes conjuntos de datos y determinar los r valores. 

Estudiante: ¡Fabuloso! Ahora entiendo mucho más lo de Rectas de mejor ajuste, y puedo predecir los r-valores de diagramas de dispersión.