Inicio Actividades Cálculo Transmógrafo en 3D
Transmógrafo en 3D
Temas
Transmógrafo en 3D
¿En qué consiste la actividad Transmógrafo en 3D ?
Esta aplicación es una versión ampliada de Transmógrafo y Transmógrafo 2. Es un modelo 3D que permite explorar el mundo de las traslaciones, reflexiones y rotaciones.
La aplicación permite al usuario trasladar polígonos en las direcciones de los ejes x y y. También puede reflejar la figura a través de cualquier recta
y=mx+b
donde m es la pendiente y b es el intercepto en el eje y. Por ejemplo, un polígons reflejado a través de la recta y=2x+1 se ve como esto: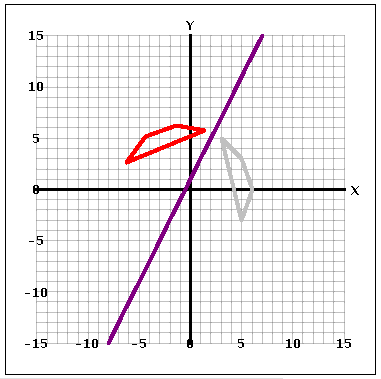
El usuario también puede reflejar la figura a través de una recta verticasl de ecuación x=? en la que ? es remplazada por cualquier entero tal que la imagen reflejada cae en el interior de la gráfica. Aquí se muestra por ejemplo un polígono reflejado en la recta x=0.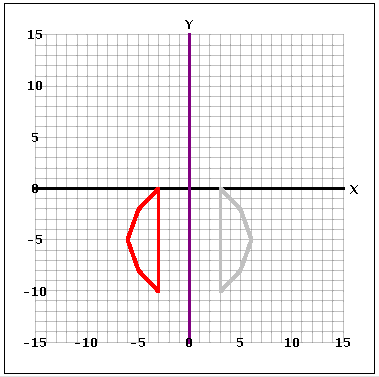
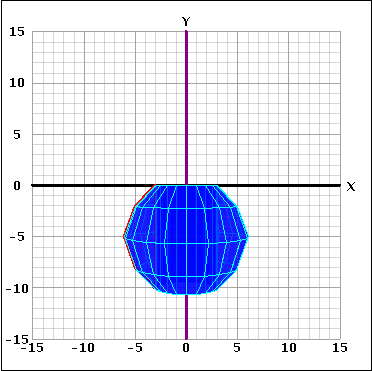
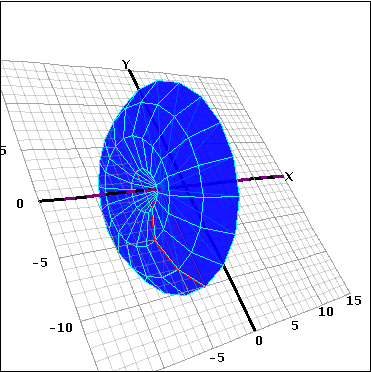
Esta aplicación es 3D porque se ha añadido una función de revolución que permite al usuario girar un polígono a través del plano z alrededor de una recta del plano x-y. En lugar de rotar el polígono, el botón de revolución permite apreciar cómo se vería el polígono si estuviera girando alrededor de un eje en el espacio tridimensional. Al hacer click en el gráfico y arrastrarlo, el usuario puede tener una idea mucho mejor de la forma del objeto tridimensional. El mismo polígono de arriba reflejado sobre el eje y se ve así:
y cuando gira alrededor del eje x se ve así: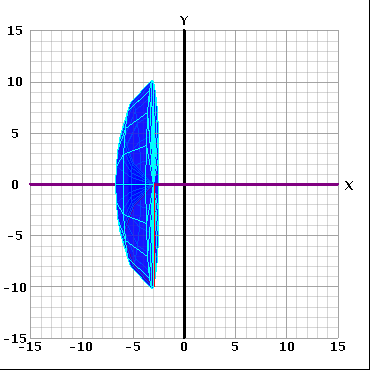
Usted puede ver que estas imágenes son muy diferentes. Cambiando la vista de los ejes - haciendo click y arrastrando-, se tiene una mejor apreciación de sus formas.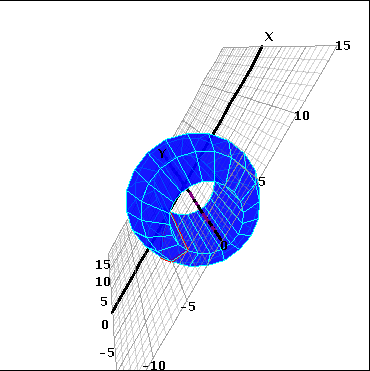
Recursos para la clase
- Actividad Función de Revolución
- Actividad Transmógrafo
- Actividad Transmógrafo 2
- Discusión sobre Introducción al plano coordenado y coordenadas
- Discusión sobreTraslaciones, Reflexiones y Rotaciones
- Taller Transformaciones
- Taller Transformaciones(doc)
- Taller Traslaciones, Reflexiones y Rotaciones
- Taller Traslaciones, Reflexiones y Rotaciones(doc)
Actividad
¿Cómo puedo utilizar esta actividad?
Descripción
Esta aplicación le permite al usuario explorar el mundo de las traslaciones, reflexiones y rotaciones. Puede transformar polígonos con hasta 12 vértices definidos por el usuario en el plano coordenado.
Controles y Resultados
- Información general:
- Cada vértice del polígono tiene un color diferente para ayudarle a ver la orientación del polígono. Cuando usted realiza una traslación, reflexión o rotación, el polígono aparece dibujado en su nueva posición y orientación, y un polígono "fantasma" se dibuja en color gris en su posición anterior. Esto le ayuda a recordar dónde estaba el polígono antes de la transformación. También se puede manipular la perspectiva de la gráfica, arrastrándolo con el ratón. La gráfica está limitada a lo que pueda verse en la cuadrícula [(-15, 15)] a [(15, 15)]. No se permiten polígonos que excedan estas cotas y tampoco transformaciones que harían excederlas.
- Creando un nuevo polígono:
- Para crear un nuevo polígono, utilice el panel que hay junto al plano coordenado, llamado "Nuevo polígono" Ingrese el número de vértices que quiere para el nuevo polígono (entre 3 y 12) en el campo titulado "Nuevo poligono" y haga click en el botón ¡Vamos!
- Como respuesta verá un nuevo panel de dos columnas de cajas de texto: una para las coordenadas x y otra para las coordenadas y.
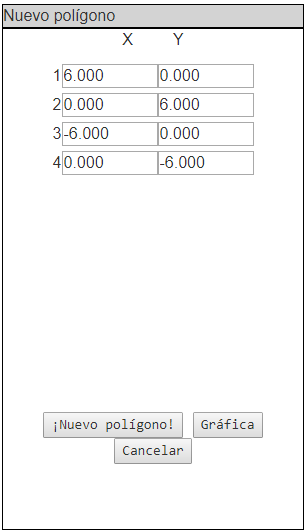
- Para crear un nuevo polígono, utilice el panel que hay junto al plano coordenado, llamado "Nuevo polígono" Ingrese el número de vértices que quiere para el nuevo polígono (entre 3 y 12) en el campo titulado "Nuevo poligono" y haga click en el botón ¡Vamos!
Ingrese las coordenadas de cada vértice. Todas las coordenadas deben ser enteras y estar entre (-15, -15) y 15, 15). Cuando lo haga, obtenga una vista previa de la figura en el plano coordenado, haciendo click en el botón Gráfica. Si quiere cambiar el número de vértices haga click en el botón Nuevo polígono. Este nuevo polígono será dibujado en el plano coordenado.
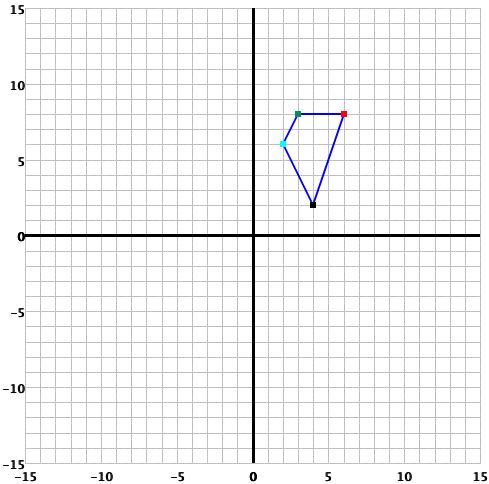
Si no está satisfecho con esta figura y quiere volver a la figura original , presione el botón Cancelar
Controles de traslación
- Digite en los espacios apropiados el número de unidades en que quiere trasladar la figura en las direcciones de los ejes X y Y. El panel está abajo del plano coordenado y se ve así:

- Ambos números deben ser enteros. A continuación haga click en el botón (Trasladar) para trasladar el pológono. Si la traslación está entre los límites de la cuadrícula, aparecerá en el plano coordenado como:
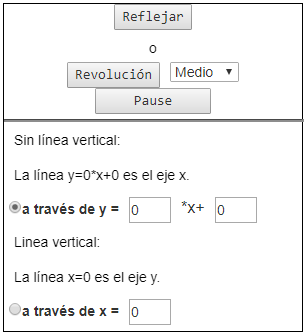
Controles de Reflexion:
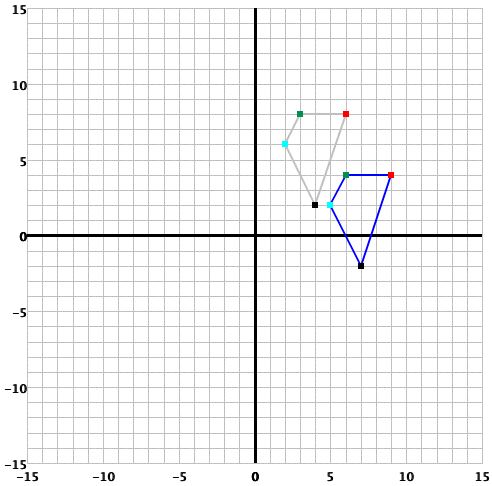
- Para reflejar a través de una recta no vertical, haga click en el círculo que hay junto al texto "a través de y=" e ingrese la pendiente y el -intercepto de la recta en la que se hará la reflexión (ambos números deben ser enteros).Esto se encuentra debajo del plano de coordenadas. Como ilustración, el siguiente ejemplo producirá una reflexión en la recta y=2x+5 cuando haga click en el botón Reflejar.
- La gráfica de esta reflexión es:
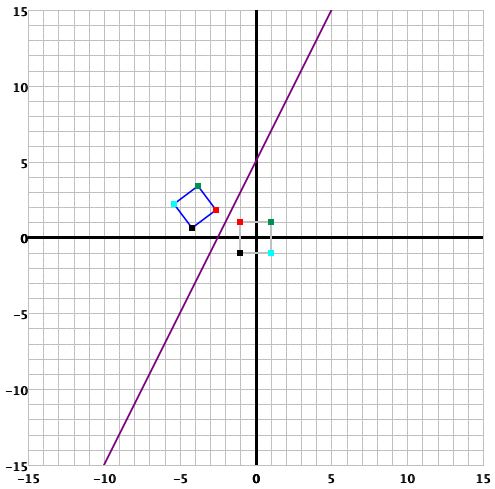 :
:
Para reflejar a través de una recta vertical, haga click en el círculo que hay junto al texto "a través de x=" e ingrese la coordenada x de la recta en la que se hará la reflexión (este número debe ser entero).Esto se encuentra debajo del plano de coordenadas. Como ilustración, el siguiente ejemplo producirá una reflexión a través de la recta x=3 cuando haga click en el botón Reflejar.

- La gráfica de esta reflexión es:
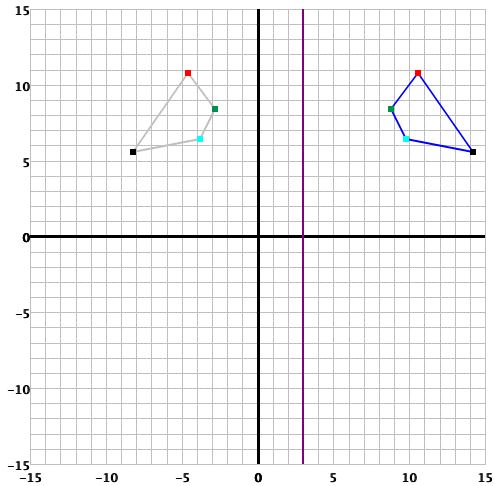
-
- Solamente las reflexiones que se ajusten a los límites de la cuadrícula serán desplegadas. Si se intenta una reflexión que exceda tales límites, aparecerá una caja de texto explicativo.
- Solamente las reflexiones que se ajusten a los límites de la cuadrícula serán desplegadas. Si se intenta una reflexión que exceda tales límites, aparecerá una caja de texto explicativo.
- Controles de revolución:
- Estos controles operan en forma similara a los de reflexión. Para girar un objeto alrededor de una recta no vertical haga click en el círculo que hay junto al texto "a través de y=" e ingrese la pendiente y el -intercepto de la recta que desea girar (ambos números deben ser enteros).Esto se encuentra debajo del plano de coordenadas. Como ilustración, el siguiente ejemplo producirá un giro alrededor de la recta y=2x+5 cuando haga click en el botón de Revolución como se ve en el gráfico siguiente:
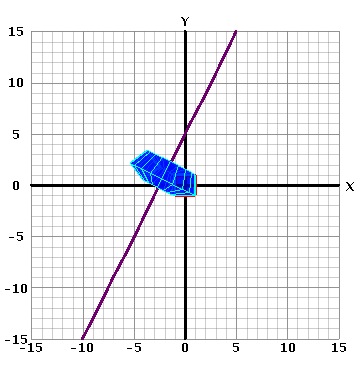
-
- Se puede graduar la velocidad en la que se construye el sólido, seleccionando una de las opciones que se encuentran al lado del botón Revolución y posterior mente presionando este.

- Se puede graduar la velocidad en la que se construye el sólido, seleccionando una de las opciones que se encuentran al lado del botón Revolución y posterior mente presionando este.
- Controles de rotación:
- Ingrese el número de grados (debe ser un entero) para la rotación del poligono en el campo apropiado. A continuación, ingrese las coordenadas x, y del centro de rotación, que deben ser números enteros y haga click en el botón Rotar. El panel para la rotación es así:
- Y esta es la gráfica de una rotación:
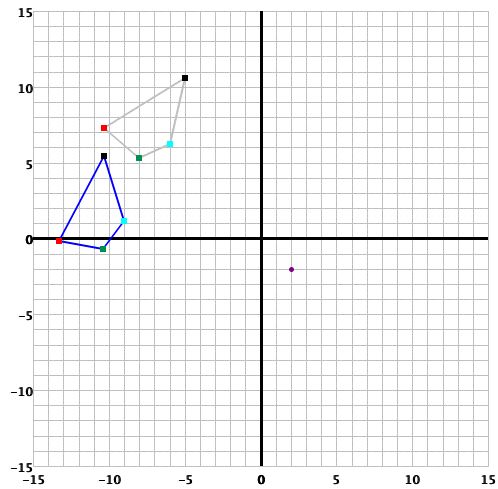
- Solamente las rotaciones que se ajusten a los límites de la cuadrícula serán desplegadas. Si se intenta una rotación que exceda tales límites, aparecerá una caja de texto explicativo.
- Manipulando la forma en que se ve la gráfica
- Haciendo click y arrastrando la gráfica usted puede cambiar la forma en la que se ve. Su perspectiva no está limitada a un eje en particular. Para volver a la vista predeterminada haga click en el botón Restablecer la vista. Este botón no le funcionará si la vista actual es la vista predeterminada.
Recursos y contexto curricular
Esta aplicación es una versión ampliada de Transmógrafo y Transmógrafo 2. Es un modelo 3D que permite explorar el mundo de las traslaciones, reflexiones y rotaciones.
La aplicación permite al usuario trasladar polígonos en las direcciones de los ejes x y y. También puede reflejar la figura a través de cualquier recta
y=mx+b
donde m es la pendiente y b es el intercepto en el eje y. El usuario también puede reflejar la figura a través de una recta vertical de ecuación x=? en la que ? es remplazada por cualquier entero tal que la imagen reflejada cae en el interior de la gráfica.
Esta aplicación también permite rotar el polígono alrededor de un punto cualquiera en el plano o un número dado de grados. Cuando se quiera ver la gráfica en 3D simplemente se hace click en la gráfica y se arrastra hasta obtener la vista deseada.
Esta actividad se desarrolla bien en grupos de 2 o 3 estudiantes para que entiendan mejor los conceptos antes de poder trabajar en ellos independientemente.
Ubicación en el currículo de matemáticas
- presentar los conceptos de traslación, reflexión y rotación de una gráfica
- Mostrar cómo dibujar formas básicas en el sistema de coordenadas cartesianas.
- desarrollar las habilidades de visualización mental en los estudiantes.
- practicar la traslacióin, reflexión y rotación de objetos 3D en el plano de coordenadas.
Estándares alcanzados
Grados 6-8
- Geometría
- Aplicar transformaciones y usar simetría para analizar situaciones matemáticas.
- Especificar posiciones y describir relaciones espaciales usando geometría de coordenadas y otros sistemas de representación.
Grados 9-12
- Geometría
- Aplicar transformaciones y usar simetría para analizar situaciones matemáticas.
Esté preparado para:
- definir traslaciones, reflexiones y rotaciones y mostrar ejemplos
- explicar traslacion y rotación en general.
Recursos para clases
- Actividad Función de Revolución
- Actividad Transmógrafo
- Actividad Transmógrafo 2
- Discusión sobre Introducción al plano coordenado y coordenadas
- Discusión sobre Traslaciones, Reflexiones y Rotaciones
- Lección sobre Sistema de coordenadas cartesianas
- Lección sobre Transformaciones (Básica primaria)
- Lección sobre Traslación, reflexión, y rotación
- Taller Transformaciones
- Taller Transformaciones(doc)
- Taller Traslaciones, Reflexiones y Rotaciones
- Taller Traslaciones, Reflexiones y Rotaciones(doc)
