Inicio Actividades Trigonometría Cuadratura del triángulo
Cuadratura del triángulo
Temas
Cuadratura del triángulo
¿En qué consiste la actividad Cuadratura del triángulo ?
Esta “simulación” permite al usuario explorar triángulos rectángulos y el teorema de Pitágoras. También puede usarse para explorar con medidas de los ángulos de los triángulos.
Pitágoras, a quien debe su nombre el teorema, era un filósofo y científico griego. El teorema dice que en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los dos catetos , es decir, de los otros dos lados del triángulo.
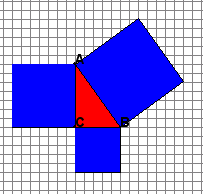
Para que el usuario pueda estudiar las relaciones involucradas en el teorema de Pitágoras, esta “simulación” dibuja un cuadrado en cada uno de los lados del triángulo. A medida que el usuario ajusta la longitud de un lado del triángulo, el cuadrado se ajusta automáticamente. La información descriptiva sobre la longitud de cada uno de los lados, la medida de cada ángulo, y el área de cada cuadrado, es suministrada en la “simulación”.
Recursos para la clase
Actividad
¿Cómo puedo utilizar esta actividad?
Descripción
Esta “simulación” permite al usuario explorar triángulos rectángulos y el teorema de Pitágoras. También puede usarse para explorar medidas de los ángulos de los triángulos.
Controles y Resultados
El objetivo de esta actividad es desarrollar un buen conocimiento del teorema de Pitágoras. La “simulación” muestra un triángulo rectángulo en cada uno de cuyos lados se ha construido un cuadrado con los lados de igual longitud al lado del triángulo sobre el cual está construido. Al variar ó ajustar la longitud de los lados del triángulo, el usuario puede experimentar visualmente el teorema de Pitágoras.
Controles y resultados
- Al hacer ajustes a las barras de movimiento, el usuario puede cambiar la longitud de las bases del triángulo rojo:

- Observe cómo el triángulo cambia y cómo también lo hace el área de los cuadrados. ¿Cuál es la relación entre los cuadrados?
- La información en la parte inferior de la “simulación” se suministra para ayudar al usuario a entender las relaciones entre el área de los cuadrados y la longitud de los lados. El usuario también podrá descubrir algunas características de la naturaleza de los ángulos en los triángulos.

Recursos y contexto curricular
Esta actividad permite al usuario investigar las ideas fundamentales en las que se basa el teorema de Pitágoras y la naturaleza de los triángulos. Si usted utiliza las preguntas de exploración esta actividad funcionará bien con grupos de 2 estudiantes y les tomará unos 20 o 30 minutos; de lo contrario, requerirá unos 5 o 10 minutos.
Ubicación en el currículo de matemáticas
Esta actividad se puede usar para:
- Presentar el teorema de Pitágoras.
- Explorar el concepto de área.
- Explorar la naturaleza de los ángulos en los triángulos.
Estándares alcanzados
- Estándar de números y operaciones
- Comprender el significado de las operaciones y cómo se relacionan entre sí.
- Hacer cálculos con facilidad y hacer estimativos razonables.
- Estándar de álgebra
- Representar y analizar situaciones y estructuras matemáticas utilizando símbolos algebraicos.
- Estándar de geometría
- Analizar características y propiedades de formas geométricas de dos y tres dimensiones y desarrollar argumentos matemáticos sobre relaciones geométricas.
Esté preparado para:
- Dar instrucciones implícitas sobre lo que los estudiantes deben hacer. Por ejemplo “hoy vamos a jugar con el “simulación” “Cuadratura del triángulo”. Esteremos buscando patrones en el área de los cuadrados, los ángulos, … y veremos qué descubrimos.”
- Discutir el teorema de Pitágoras y definir hipotenusa.
