WebQuest Matemáticas Álgebra Lenguaje Algebraico
Lenguaje Algebraico
Publicado el 30 Mayo de 2014
Autor: Didier Antonio Sequeda Martínez
Introducción
Al momento de la interiorización de los nuevos aprendizajes, es fundamental recurrir a los aprendizajes previos del dicente, retomar lo que el estudiantes ya conoce y maneja esto es necesario adaptarlo a los nuevos saberes. una de las transiciones de mas dificultad en los estudiantes es la del paso de la Aritmética - al Álgebra, es hay donde nace la mayor fobia por las matemáticas. Si no se fundamenta la aritmética y se maneja con total solvencia por parte del estudiante, es hay donde se agudiza el problema ya que esos sabes ya o se recuerdan poco o fueron olvidados y en muchos casos ni existieron.
En el grado octavo es donde se presenta el mayor porcentaje de perdidas en el área de Matemáticas debido a este problema, es por eso fundamental realizar avances, pero infiriendo en lo ya visto (pre-saberes) y en muy pocas ocasiones aprendido, ya que la relación constante entre lo conocido y lo nuevo por conocer nos lleva a una adaptación significativa y estable.
El lenguaje algebraico es el comienzo de este proceso es donde impartimos al estudiante los conceptos básicos y fundamentales sobre el álgebra es aquí donde se debe relacionar a profundidad todas las temáticas vistas y las por ver, se hace introducción por primera ves a la letra con valores variantes (las variables), se definen las operaciones básicas con la utilización de la letra y el número.
Ficha técnica
Área:Matemáticas
Asignatura:Álgebra
Edad: No hay restriccion de edad
Herramientas:
Auto Aplicaciones
Bases de datos
Blogs
Calendarios
Etiquetado social
Fotografía
Gráficas
Infografías

Crear proyectos de clase utilizando inteligencia artificial dando clic aquí
Tarea
Miremos Como se construye una expresión algebraica.
Para poder manejar el lenguaje algébrico es necesario comprender lo siguiente:
- Se usan todas las letras del alfabeto.
- Las primeras letras del alfabeto se determinan por regla general como constantes, es decir, cualquier número.
- Por lo regular las letras X., Y y Z se utilizan como las incógnitas o variables de la función o expresión algebraica.
Actividad 1.
Realiza las siguientes operaciones teniendo en cuenta el valor asignado para cada letra .
Si x=2 y z=5 realiza las operaciones indicadas.
- x+z
- 9x - 5z
- z/y
- 8z4
- xz
- x4/z7
Actividad 2
Operaciones con Lenguaje AlgebraicoEncuentra cual expresión algebraica representa el enunciado.
- La mitad de un número.
B) x²
C) x/2
- El doble de un número más tres
B) 2(x + 3)
C) 2x + 3
- El triple de un número menos cuatro
B) 3 · 4 - x
C) 3x - 4
- la mitad del cubo de un número
B) x3/2
C) 3 · x /2
- Siete menos un número
B) 7 - x
C) x - 7
- El doble de la suma de dos números
B) m + n · 2
C) 2 · m + n
- La edad de una persona hace cinco años
B) 5 - x
C) 32 - 5
- El cuadrado más el triple de un número
B) x + 32
C) 32 + 3x
- La quinta parte del triple de un número
B) 3 · 5 /x
C) x/3 · 5
- El triple de la suma de tres números
B) 3 + a + b + c
C) a + b + c · 3
Actividad 3.
En el siguiente listado de frases completa el lenguaje o su contenido matemático:
| Frase | Expresión algebraica |
| La suma de 2 y un número | |
| 3 más que un número | x + 3 |
| a - 5 | |
| 4 menos que n | 4 - n |
| k + 1 | |
| Un número disminuido en 10 | |
| a • b | |
| Dos veces la suma de dos números | |
| 2a + b | |
| Cinco veces un número | |
| n multiplicado por el número conocido | |
| El cociente de dos números | |
| La suma de dos números | |
| n + 10 | |
| Un número aumentado en 3 | |
| a – 2 | |
| El producto de p y q | |
| n – 1 | |
| El antecesor de un número cualquiera | |
| x + 1 | |
| 3 veces la diferencia de dos números | |
| 10 + 3b | |
| La diferencia de dos números | |
| 24 + 19 = 43 | |
| 19 más que 33 | |
| 2(9 – 4) = 18 – 8 = 10 | |
| El producto de 6 y 16 | |
| 3(27 – 21) = 81 – 63 = 18 | |
| La diferencia de 9 al cuadrado y 4 al cuadrado | |
| 33 / 9 = 27 / 9 = 3 | |
| 12 al cuadrado dividido por el producto de 8 y 12 |
Procesos
Operaciones con Lenguaje AlgebraicoMiremos algunas de las situaciones más comunes que involucran los problemas de matemáticas con lenguaje algebraico.
- Un número cualquiera
se puede denominar con cualquier letra del alfabeto, por ejemplo:
a = un número cualquiera, b = un número cualquiera, c = un número cualquiera. Y así sucesivamente con todos los datos del alfabeto.
- La suma de dos números cualesquiera
a+b = la suma de dos números cualesquiera
x+y = la suma de dos números cualesquiera
- La resta de dos números cualesquiera
a-b = la resta de dos números cualesquiera
m-n = la resta de dos números cualesquier
- El producto de dos números cualesquiera
ab = el producto de dos números cualesquiera
- El cociente de dos números cualesquiera (la división de dos números cualesquiera)
a/b= el cociente de dos números cualesquiera.
Ahora al momento de utilizar expresiones algebraicas tenemos que.
El lenguaje que usamos en operaciones aritméticas en las que sólo intervienen números se llama lenguaje numérico.
En ocasiones empleamos letras para representar cualquier número desconocido, realizamos operaciones aritméticas con ellas e, incluso, las incluimos en expresiones matemáticas para poder calcular su valor numérico.
El lenguaje que utiliza letras en combinación con números y signos, y, además, las trata como números en operaciones y propiedades, se llama lenguaje algebraico.
La parte de las Matemáticas que estudia la relación entre números, letras y signos se llama Álgebra.
Características del lenguaje algebraico.
1.- El lenguaje algebraico es más preciso que el lenguaje numérico: podemos expresar enunciados de una forma más breve.
El conjunto de los múltiplos de 5 es 5 por ±5, ±10, ±15, ...
En lenguaje algebraico se expresa 5 • n, con n un número entero múltiplo de cinco.
2.- El lenguaje algebraico permite expresar relaciones y propiedades numéricas de carácter general.
La propiedad conmutativa del producto se expresa a • b = b • a, donde a y b son dos números cualesquiera.
3.- Con el lenguaje algebraico expresamos números desconocidos y realizamos operaciones aritméticas con ellos.
El doble de un número es seis se expresa 2 • x = 6.
Expresiones algebraicas
Una expresión algebraica es un conjunto de números y letras que se combinan con los signos de las operaciones aritméticas. Una expresión algebraica se define como aquella que está constituida por coeficientes, exponentes y bases.
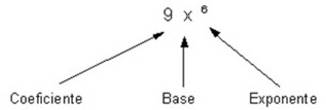
Coeficiente numérico: es la cantidad numérica o letra que se encuentra a la izquierda de la base, la cual indica la cantidad de veces que la base se debe sumar o restar dependiendo del signo que tenga.
Ejemplos:
7x4 = x4 + x4 + x4 + x4 + x4 + x4 + x4
– 3x2 = – x2 – x2 – x2
Exponente numérico: es la cantidad que se encuentra arriba a la derecha de la base, la cual indica la cantidad de veces que la base se toma como producto.
Ejemplos:
5x3 = 5 (x) (x) (x)
8( – x + 5)2 = 8(– x + 5) (– x + 5)
Valor numérico de una expresión algebraica
El valor numérico de una expresión algebraica es el número que resulta de sustituir las letras por números y realizar a continuación las operaciones que se indican.
Una cantidad desconocida se puede representar con alguna letra llamada variable.
Recursos
.
Evaluación
Para las actividades, la valoración se medirá en una escala de 1 a 5
Actividad 1: 20 %
Actividad 2: 30%
Actividad 3: 30%
Participación 10%
Auto Evaluación 10%
Nota del educando, según su evolución y rendimiento en las actividades.
Notas
Institución Educativa Técnico Industrial Antonio Prieto (IETIAP)
Sincelejo-Sucre, Colombia.
Creditos
Didier Antonio Sequeda MartÍNez - Utilizando A Eduteka.org

*Nota: toda la información que aparece en los Proyectos de Clase y WebQuest del portal educativo Eduteka es creada por los usuarios del portal.
