LOS MANIPULABLES EN LA ENSEÑANZA DE LAS MATEMÁTICAS
Mediante el método mecánico logré entender ciertos resultados,
aunque posteriormente tuviesen que ser demostrados geométricamente
ya que la investigación mediante el método mecánico no proveía las demostraciones.
Pero es mucho más fácil poder dar una demostración de una situación,
después de haberla comprendido mediante el mencionado método
que intentar demostrarla sin ningún conocimiento previo.
Arquímedes
Inventor, Físico y Matemático Griego (287-212 a.C.)
Bajo la denominación de Manipulables se agrupan una serie de ayudas tanto físicas como virtuales que facilitan el aprendizaje.
Un Manipulable para matemáticas puede entrar en dos categorías:
1) Físicos, que se definen como cualquier material u objeto físico del mundo real que los estudiantes pueden “palpar” para ver y experimentar conceptos matemáticos. Los instrumentos de este tipo se utilizan principalmente con los estudiantes de los primeros grados escolares y ejemplos de ellos son: Formas Geométricas para el reconocimiento de las distintas figuras; Bloques de Patrones para estimar, medir, registrar, comparar; Bloques y Cubos para sumar, restar o resolver problemas que incluyen peso.
2) Virtuales, que se definen como representaciones digitales de la realidad posibilitadas por los computadores, y que el estudiante puede también manipular con el mismo objetivo de los primeros. Estos últimos se utilizan en los grados superiores. La experta Judy Spicer ha dicho: “Los manipulables virtuales tienen además la capacidad de hacer visible lo que es difícil de ver e imposible de imaginar” [1]. Ejemplos de éstos son: Simulaciones; Software de Visualización; Fractales; Robótica; Juegos de Computador; Representaciones Tridimensionales; etc.
USO DE MANIPULABLES VIRTUALES
Los manipulables bien diseñados y bien utilizados (físicos o virtuales) ayudan a los estudiantes a construir, fortalecer y conectar varias representaciones de ideas matemáticas al tiempo que aumentan la variedad de problemas sobre los que pueden pensar y resolver.
Asimismo, los Manipulables ofrecen a los estudiantes objetos para reflexionar y hablar. Les suministran un lenguaje adicional para comunicar ideas matemáticas sobre sus percepciones visuales, táctiles y espaciales.
Investigaciones adelantadas en Inglaterra, Japón, China y Estados Unidos soportan esta idea [2]. En estas se enfatiza especialmente la ayuda que ofrecen a los estudiantes para pasar del nivel concreto al abstracto e incrementar su capacidad para adquirir habilidades y conceptos al ofrecer una representación física, tangible, móvil, armable y desarmable, que permite visualizar conceptos matemáticos de manera concreta. Dice también la investigación que los niños pasan por tres estadios de desarrollo: el concreto o de manipulación, el representativo o de transición y el abstracto. Muchos estudiantes tienen gran dificultad para hacer esta transición, posiblemente porque su sentido numérico es débil. “Piaget encontró que la mayoría de los niños no alcanzan el nivel abstracto sino a la edad de 12 o 14 años. Para respaldar el avance de la etapa de transición a la abstracta, es necesario ofrecer a los estudiantes materiales y actividades apropiadas para lograrlo y en el caso de las matemáticas, éste papel lo asumen los manipulables. Además, se encontró que los estudiantes que aprenden matemáticas con este tipo de modelos entienden mejor, desarrollan mejores habilidades para la solución de problemas y tienen un mejor desempeño en las pruebas estandarizadas de competencia” [3].
Los resultados más interesantes encontrados por las investigaciones sobre cómo la tecnología puede mejorar el aprendizaje, se enfocan en manipulables virtuales que ayudan a los estudiantes a entender conceptos esenciales en áreas como matemáticas o ciencias mediante la representación de temas, en forma más sencilla. Las investigaciones han demostrado que la tecnología puede impulsar profundos cambios en lo que aprenden los estudiantes. Utilizando la capacidad del computador para posibilitar simulaciones, enlaces dinámicos e interactividad, el estudiante regular puede alcanzar un dominio extraordinario de conceptos sofisticados. Algunos de estos manipulables (Visualizaciones, Modelos y Simulaciones) han probado ser herramientas poderosas para enseñar conceptos matemáticos y científicos.
Por ejemplo, la tecnología que utiliza diagramas dinámicos (esto es, imágenes que pueden moverse en respuesta a un rango de comandos u órdenes) puede ayudar a que los estudiantes visualicen y entiendan las fuerzas que subyacen en varios fenómenos. El estímulo a los estudiantes para buscar el sentido de las simulaciones que modelan fenómenos físicos, pero que desafían las explicaciones intuitivas, ha demostrado ser también una técnica útil. Ejemplo de esto son simulaciones que permiten visualizar conceptos cómo velocidad y aceleración.
Buscando técnicas que incrementen la matemática que pueden aprender los estudiantes, los investigadores han encontrado que desplazarse de las expresiones matemáticas que se formulan con lápiz y papel (tales como símbolos algebraicos) a las que se plantean en la pantalla (que incluyen no solamente símbolos algebraicos, sino también gráficas, tablas y figuras geométricas) puede tener un efecto positivo dramático.
En lugar de usar lápiz y papel con los que solamente se representan expresiones matemáticas estáticas y aisladas, que se usan por lo general para realizar cálculos, los maestros de matemáticas están dirigiendo cada vez más sus esfuerzos a facilitar que el estudiante comprenda y adquiera conceptos en lugar de dedicarse únicamente a realizar procedimientos mecánicos. La utilización de computadores que posibilita el uso de manipulables virtuales ofrece para éste último objetivo varias ventajas
Beneficios Pedagógicos Prácticos:
-
Son más reales que los ejercicios escritos o las descripciones de fenómenos.
-
Priorizan el proceso de pensamiento del estudiante a medida que éste construye conocimiento matemático.
-
Posibilitan mediante retroalimentación el establecimiento de vínculos entre lo concreto y lo simbólico.
El estudiante puede diseñar objetos, moverlos y modificarlos, y expresar esas acciones en números o palabras. -
Promueven y facilitan explicaciones completas y precisas ya que el estudiante debe especificarle al computador, con precisión, lo que debe hacer para obtener resultados concretos.
-
Se pueden crear, por ejemplo, tantas copias de una forma geométrica como sea necesario, y usar herramientas del computador para mover, combinar y duplicar estas formas para hacer figuras, diseños y solucionar problemas.
-
Los productos realizados pueden guardarse y recuperarse a voluntad, sin tener que “perder” todo el trabajo que se ha realizado, permitiendo además, trabajarlo una y otra vez.
-
Se pueden diferenciar las diversas formas de varias maneras (colores, fondos, etc).
-
Estas aplicaciones son más limpias, manejables y flexibles; siempre están en la posición correcta y se quedan donde se colocan, se pueden “congelar” en la posición deseada.
-
Son una manera mucho más motivadora que trabajar con lápiz y papel.
-
Muchas construcciones son más fáciles de construir que con elementos físicos.
-
Ofrecen la posibilidad de guardar y recuperar una serie de acciones realizadas con anterioridad por el estudiante pero que pueden trabajarse más. Se pueden recuperar secuencias de acciones.
-
Permiten obtener un registro del trabajo con mucha facilidad. Se puede imprimir.
Beneficios Matemáticos:
-
Hacer conscientes ideas y procesos matemáticos en los estudiantes.
-
Permitir a los estudiantes razonar mientras manipulan en el computador gráficas o figuras dinámicas y las expresiones matemáticas relacionadas con éstas.
-
Explorar, gracias a la flexibilidad de los manipulables, las figuras geométricas de maneras que no son posibles con figuras físicas (cambios en forma o tamaño, cambios generales o particulares, etc).
-
Facilitar la exploración rápida de los cambios en las expresiones matemáticas con el simple movimiento del ratón, en contraposición de lo que sucede cuando se utiliza lápiz y papel.
-
Visualizar los efectos que tiene en una expresión matemática, modificar otra. Por ejemplo, cambiar el valor de un parámetro de una ecuación y ver cómo la gráfica resultante cambia de forma.
-
Acelerar la exposición a un gran número de problemas y ofrecer retroalimentación inmediata.
-
Relacionar con facilidad símbolos matemáticos, ya sea con datos del mundo real o con simulaciones de fenómenos corrientes, lo que le da significado a las matemáticas.
-
Obtener retroalimentación inmediata cuando los estudiantes generan expresiones matemáticas incorrectas.
-
Realizar procesos de composición y descomposición de formas (realizar unidades compuestas, descomponer un hexágono en otras formas cómo triángulos, etc).
-
Conectar el aprendizaje Geométrico/Espacial al aprendizaje numérico, relacionando dinámicamente ideas y procesos numéricos con las ideas de los estudiantes sobre formas y espacio.
-
Permitir que se detenga la aplicación en cualquier momento del proceso si se requiere tiempo para pensar sobre éste. Además, puede repetirse si se desea ver nuevamente parte de esta o ensayar otras respuestas.
TIPOS DE MANIPULABLES VIRTUALES
Los siguientes son algunos ejemplos de Manipulables Virtuales.
SIMULACIONES: Una de las formas más efectivas y fáciles de integrar las TICs en las materias del currículo es mediante el uso de simulaciones. Muchas de estas se encuentran disponibles en Internet para propósitos educativos, en la mayoría de los casos sin costo. Algunas son interactivas, es decir, que permiten al estudiante modificar algún parámetro y observar en la pantalla el efecto producido por dicho cambio. Otras posibilitan además configurar el entorno, esto es, que los educadores pueden programarlas para que aparezcan distintos elementos y diferentes tipos de interacciones. Una de las cualidades que poseen las Simulaciones es el alto grado de motivación que despiertan en los estudiantes y poder llegar a resultados a través de un proceso de ensayo y error (orientado por el profesor). Este proceso les permite descubrir conceptos matemáticos e ir construyendo un puente entre las ideas intuitivas y los conceptos formales. En EDUTEKA ofrecemos varios Módulos de simulaciones para Matemáticas, Física y Estadística, presentadas en módulos listos para descargar, que pueden utilizarse para cubrir contenidos específicos, facilitando de esta manera su integración a las estrategias didácticas usadas por el educador (http://www.eduteka.org/instalables.php).
También se ofrece una reseña de sitios que ofrecen excelentes simulaciones.
SOFTWARE DE VISUALIZACIÓN: La visualización juega un papel muy importante en la enseñanza de las Matemáticas y su mayor impacto se logra cuando los estudiantes logran visualizar un concepto o problema. “Visualizar un problema significa entenderlo en términos de un diagrama o de una imagen visual. La visualización en matemáticas es un proceso en el que se forman imágenes mentales con lápiz y papel, o con la ayuda de tecnología, y se utiliza con efectividad para el descubrimiento y comprensión de nociones matemáticas” [4].
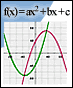
Dos áreas de la Matemática en las cuales este tipo de Manipulables hace grandes aportes son el álgebra y la geometría. El Álgebra es un medio de representación en el cual se trasladan relaciones cuantitativas a ecuaciones o gráficas. El uso de software o de calculadoras para graficar funciones ayuda a los estudiantes a ver las ecuaciones y sus soluciones con una nueva perspectiva, más allá de su solución algorítmica (abstracta). Por ejemplo, los modelos interactivos que ofrece ExploreMath (http://www.exploremath.com/activities/index.cfm) posibilitan al estudiante visualizar y manipular diversas variables para resolver problemas relacionados con el plano cartesiano, funciones (lineales, cuadráticas y polinomiales), desigualdades, valor absoluto, etc. La función gráfica de la Hoja de Cálculo permite a los estudiantes resolver igualdades y desigualdades favoreciendo la comprensión de los conceptos mediante la observación gráfica de resultados numéricos (ver http://eduteka.org/HojaCalculo1.php).
En Geometría, programas como Cabri Géomètre (http://www-cabri.imag.fr/index-e.html) o Geometer's Sketchpad (http://www.keypress.com/sketchpad/) generan una nueva forma de realidad virtual asociada a los objetos conceptuales de las Matemáticas y además los traen a la pantalla en donde los estudiantes pueden manipularlos libremente. Esta manipulación del entorno geométrico permite al estudiante ampliar su experiencia en esta disciplina y validar enunciados matemáticos, algo que es muy difícil de lograr sin la mediación de este tipo de software [5].
FRACTALES: Voz inventada por el matemático francés B. Mandelbrot en 1975. Son figuras planas o espaciales, compuestas de infinitos elementos, que tienen la propiedad de no cambiar su aspecto y distribución estadística cualquiera que sea la escala con que se observen [6]. En el sitio creado por Cynthia Lanius (http://math.rice.edu/~lanius/frac/) se pueden explorar ejemplos de fractales, actividades e instrucciones. Las actividades ilustran la iteración y autosimilitud característica de estas figuras; por ejemplo, en el “Triángulo Sierpinski” (figura 1) los puntos medios de los lados de un triángulo equilátero están conectados con tres líneas, formando cuatro triángulos similares al original y creando un patrón de menor tamaño compuesto por triángulos más pequeños.
 |
| Figura 1: Triángulo Sierpinski |
También te podría interesar
El Principio de la tecnología para matemáticas escolares
Ver artículoLa propuesta de los Centros de Aprendizaje en la sociedad de la información
Ver artículoHerramientas de las TIC que contribuyen a formar para la ciudadanía
Ver artículoUn docente que utiliza TIC para enseñar Matemáticas
Ver artículo
REPRESENTACIONES TRIDIMENSIONALES: Los computadores hacen posible la creación de imágenes interactivas de objetos tridimensionales que se pueden rotar y cambiar de posición para facilitar su estudio. En el sitio creado por George W. Hart (http://www.georgehart.com/) hay una colección de poliedros virtuales que se pueden manipular. Estas imágenes tridimensionales están construidas con VRML (Virtual Reality Modeling Language) y para visualizarlas en el computador, se debe instalar un programa que soporte archivos del tipo “.wrl”. Hay una lista muy completa de fabricantes de estos programas en la dirección: http://www.web3d.org/vrml/browpi.htm Uno de ellos es “Alice”, creado por la Universidad Carnegie Mellon el cual se puede descargar gratuitamente: http://www.alice.org/ Con JavaSketchpad DR3 Gallery (http://www.dynamicgeometry.com/) los estudiantes pueden explorar 16 actividades, la mayoría forman figuras tridimensionales tales como un “hipercubo” totalmente manipulable.
JUEGOS DE COMPUTADOR: Un estudio realizado en el Reino Unido [7] concluye que los juegos de simulación y aventura desarrollan el pensamiento estratégico y las habilidades de planificación de los estudiantes. En estos juegos de computador los estudiantes deben tomar decisiones, modificar condiciones, reaccionar ante situaciones o prever ciertas circunstancias. El juego Sim City (http://simcity.ea.com/) permite a los estudiantes crear ciudades virtuales sobre las cuales ellos tienen el control. Tal como el alcalde de su ciudad, ellos aprenden qué condiciones (acueducto y alcantarillado, redes eléctricas, vías de transporte, áreas residenciales, industriales y comerciales, servicios de vigilancia y seguridad, educación, salud, cultura, recreación, etc) inciden en el éxito de una ciudad. Con este juego, en el que se deben administrar fondos municipales, se aprende a realizar y ejecutar presupuestos, a recaudar ingresos por impuestos, a direccionar estos ingresos, a ahorrar y a planificar, entre otras cosas. Para obtener resultados positivos, los estudiantes deben ser persistentes y consistentes en sus acciones a lo largo del juego. Los Sims (http://thesims.ea.com/us/index.html) es otro juego de este tipo. En él, los estudiantes crean a los habitantes de un vecindario y deben manejar sus relaciones interpersonales y laborales; satisfacer sus necesidades educativas, fisiológicas y emocionales; y crear condiciones ambientales propicias para que los personajes logren su pleno desarrollo. Todas estas variables semejantes a la realidad deben ser administradas por ellos. Zoo Tycoon (http://www.microsoft.com/games/zootycoon/) reta a los estudiantes a crear un zoológico virtual en el cual deben tener en cuenta el hábitat, la alimentación y los cuidados requeridos para cada uno de los animales exhibidos. También deben planear las instalaciones y el personal necesario para que el zoológico funcione apropiadamente. La serie Tycoon incluye juegos que simulan modelos reales de parques de atracciones, trenes, campos de golf, aeropuertos, restaurantes, etc.
ROBÓTICA: Como última categoría tenemos la Robótica que, aunque no es virtual, tiene un alto componente tecnológico. Esta da “vida” a la física, las matemáticas y la programación de computadores en forma táctil. Los Robots facilitan el aprendizaje de conceptos de razonamiento mecánico (física aplicada), promueven el espíritu creativo y desarrollan el trabajo colaborativo del estudiante. Este tipo de manipulables tienen la virtud de comprometer al estudiante en procesos de exploración, construcción de máquinas, prueba de hipótesis, realización de cambios y corrección de programas [8]. Materiales como los de Lego MindStorms (http://mindstorms.lego.com) permiten al estudiante, mediante logros sucesivos y escalonados, llegar a responder preguntas complejas o a construir teorías.
NOTAS DEL EDITOR:
[1] Spicer, Judy. October 2000. Virtual Manipulatives: A New Tool for Hands-on Math. ENC Focus 7(4) p.14.
[2] Improving Mathematics Teaching by Using Manipulatives; James w. Heddens, Kent State University.
[3] The Three Stages of Learning; Moving with Math.
[4] Álgebra de Funciones Mediante Procesos de Visualización; Vicente Carrión Miranda, Departamento de Matemática Educativa del CINVESTAV, México.
[5] “Cognición y Computación: el caso de la Geometría y la Visualización”, Luis Moreno Armella, Cinvestav – IPN, México. Artículo publicado como parte de las memorias del Seminario Nacional de Formación de Docentes: Uso de Nuevas Tecnologías en el Aula de Matemáticas”, Ministerio de Educación Nacional de Colombia, 2002.
[6] Definición tomada del Diccionario de la Lengua Española de la Real Academia Española.
[7] Teachers Evaluating Educational Multimedia (TEEM); Investigación “Los Juegos de Computador en la Educación” (en inglés, formato PDF),
[8] Gary S. Stager, “The Case for Computing”, capítulo del libro “Snapshots!, Educational Insights from the Thornburg Center”, Editado por Sara Armstrong.
CRÉDITOS:
Documento elaborado por Juan Carlos López García, editor de Eduteka, con material proveniente de varias fuentes en línea:
-
Oregon Technology in Education Council (OTEC); Artículo “Manipulables Virtuales” (en inglés), [consultado en línea, Octubre 1 de 2003]. http://otec.uoregon.edu/virtual_manipulatives.htm
-
Hartshorn, Robert and Boren, Sue (1990); Artículo “Aprendizaje Experimental de las Matemáticas: Uso de Manipulables” (en inglés), [consultado en línea, Octubre 8 de 2003]. http://www.ericfacility.net/ericdigests/ed321967.html
-
Spicer, Judy (April 13, 2000); Artículo “Manipulables Virtuales: Una Herramienta Nueva para que el Estudiante Trabaje las Matemáticas” (en inglés), [consulta en línea, octubre 8 de 2003]. http://goenc.com/
-
Resnick, M. et al. (1998); Artículo “Manipulables Digitales” (en inglés), [consulta en línea, Octubre 8 de 2003]. http://llk.media.mit.edu/projects/summaries/toys.shtml
-
Stephanie R. Schweyer (Abril 20 de 2000); Artículo “Uso Efectivo de Manipulables” (en inglés), formato pdf, [consulta en línea, Octubre 8 de 2003]. http://www.gphillymath.org/ExempPaper/Documents/manipulatives.php
-
Teachers Evaluating Educational Multimedia (TEEM); Investigación “Los Juegos de Computador en la Educación” (en inglés), [consulta en línea, Octubre 9 de 2003]. http://www.teem.org.uk/resources
-
Lipinski, Michael; Artículo “Por Qué Usar Sim City” (en inglés), [consulta en línea, Octubre 15 de 2003]. http://www.fi.edu/fellows/fellow3/apr99/simcity2000/why.htm
Publicación de este documento en EDUTEKA: Octubre 18 de 2003.
Última modificación de este documento: Octubre 18 de 2003.

Contenido publicado bajo licencia "Creative Commons"
Más sobre Los manipulables en la enseñanza de las matemáticas
MEN: Proyecto de calculadoras en la enseñanza
Conversación con la doctora Ana Celia Castiblanco Paiba, Coordinadora General del Proyecto de Incorporación de Calculadoras al Currículo de Matemáticas en Educación Básica y Media en Colombia. La funcionaria del Ministerio de Educación Nacional explica los alcances de este Proyecto.

Nueva interfaz gráfica de Matemática Interactiva
Matemática Interactiva es un recurso que permite trabajar conceptos fundamentales de Números y operaciones; Geometría y medición; Álgebra y funciones; y Estadística y probabilidad, interactivamente en línea. Buscando ampliar la utilización de este excelente recurso por un mayor número de docentes y estudiantes, modificamos la interfaz gráfica, mejorando así su navegabilidad y adicionamos a lo anterior la versión descargable. Esta puede instalarse en cualquier computador y funcionar sin necesidad de estar conectado a Internet.

Módulo Teorema de Pitágoras (.exe)
Simulaciones (applets en Java) para Matemáticas - tema: Teorema de Pitágoras - Archivo .exe (620k) descargable que instala automáticamente todos los componentes necesarios para que la simulación funcione.