Inicio Discusiones Funciones y conceptos del álgebra Variables independientes y variables dependientes
Discusiones
Temas
Variables independientes y variables dependientes
Mentor: Hoy vamos a discutir variables independientes y dependientes. ¿Qué significa que algo sea independiente?
Estudiante: Significa que no depende de algo más.
Mentor: ¡Correcto! Entonces, ¿qué significa para ti que una variable sea independiente?
Estudiante: Tal vez que esa variable no depende de otras variables o números.
Mentor: Muy bien. En érminos matemáticos, decimos que una variable es independiene si su valor puede ser asignado arbitrariamente en la obtención de un resultado. Esto se conoce como la entrada de la función. ¿Sabes qué significa "entrada" en este caso?
Estudiante: Es la variable con la que se empieza. Se conoce esa variable; entonces se hace algo con ella y se obtiene la "salida".
Mentor: Correcto. Y representamos las variables con x y con y. Cuando se da un valor a x en una ecuación, se obtiene un valor para y. Entonces, si x es la variable independiente, ¿qué nombre se le da a y?
Estudiante: Puesto que y es la salida de la función, yo creo que y sería la variable dependiente. Su valor depende del valor de x, cualquiera que este sea.
Mentor: Es correcto; y es la variable dependiente porque no asignamos un valor a y directamente; en lugar de eso, asignamos un valor a x y lo usamos para encontrar el valor de y. Considera esta sencilla ecuación como un ejemplo:
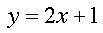
Mentor: En esta ecuación ¿cuáles son la variable independiente y dependiente?
Estudiante: Bueno, dado cualquier valor de x, hay que multiplicarlo por 2 y después sumar 1 para obtener y, es decir, y depende de x. La variable independiente es x y la variable dependiente es y.
Mentor: Cierto. Es relativamente fácil identificar las variables independiente y dependiente en una sencilla ecuación de dos variables, pero qué hacer con esta ecuación:
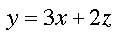
Estudiante: ¡Uff! Yo no sé qué hacer con más de dos variables. Supongo que y sigue siendo la variable dependiente, pero no sé cuál entre x y z es la variable independiente.
Mentor: Tienes razón en ambas cosas. Tanto x como z son variables independientes. Puedes cambiar cualquiera de las variables a cualquier valor antes de determinar el valor de y.
Estudiante:Ok.¡Ya lo tengo! La variable que está sola es la variable dependiente; las demás son independientes.
Mentor: Es correcto; pero...¿y si cambio un poco la ecuación? Vemos qué pasa si despejo z:
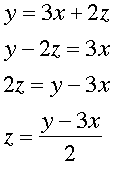
Estudiante: Entonces...z es la variable dependiente y x y y son independientes. Pero me pareció que usted dijo que y era la variable dependiente.
Mentor: Sí; lo dije, pero las variables independientes y dependientes no son inmutables, como pudieran parecerlo desde una perspectiva algebraica. En cualquier ecuación puedes escoger arbitrariamente cualquier variable como la variable dependiente, y entonces todas las demás serán variables independientes. De hecho, lo que has aprendido sobre variables independiente y dependiente tiene muy poco que ver con algebra pura.
Estudiante: Entonces, ¿por qué complicarse? ¿Por qué no decidir al azar cuál variable es independiente y cuál es dependiente?
Mentor: Piensa en la conducción de un auto. Su aceleración cambia según la presión que se ejerza sobre el acelerador y el freno y está dada en forma aproximada por la ecuación
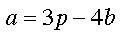
Mentor: Donde a es la aceleración, p es la presión sobre el acelerador y b es la presión sobre el freno. En esta ecuación, ¿cuál es la variable dependiente?
Estudiante: Aceleración, a es dependiente.
Mentor: Correcto, pero aún si yo reorganizara la ecuación como
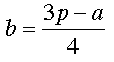
Mentor: No tendría ningún sentido decir que la presión que se ejerce sobre el freno depende de la aceleración. Obviamente es la aceleración la que depende del frenado y no al contrario. Y la presión sobre el freno ciertamente no depende de la presión sobre el acelerador.
Estudiante: Entonces, me parece que cuando usted habla de fenómenos del mundo real, los conceptos de variables independiente y dependiente se vuelven más importantes.
Mentor: Exactamente. Sobre todo cuando empiezas a aprender cómo realizar experimentos científicos la idea de variables independientes y dependientes es conceptualmente importante, asi no lo sea algebraicamente.
