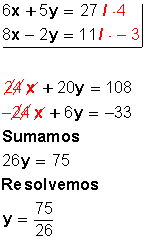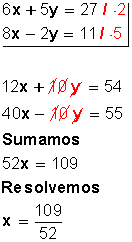Proyecto Matemáticas Álgebra Proyecto 1
Proyecto 1
Publicado el 17 Noviembre de 2015
Autor: KAREN VERGARA CARDENAS
Descripción
el proyecto tratara de los métodos para resolver ecuaciones con dos incógnitas, el fin principal es que los alumnos entiendas cada uno de los métodos para resolver un sistema de ecuaciones y los puedan utilizar de forma óptima en la resolución de sistemas de ecuaciones lineales.
objetivos:
- conocer cada uno de los métodos para resolver un sistema de ecuaciones
- aplicar cada uno de los métodos para resolver un sistema de ecuaciones
Ficha técnica
Área:Matemáticas
Asignatura:Álgebra
Edad: - No hay restriccion de edad
Duración: durará dos horas. 90 minutos
Herramientas:
Blogs
Infografías
Notice: Undefined offset: 99 in /home/edutek/www/proyectos/gp/proyecto_new/ver.php on line 160

Crear proyectos de clase utilizando inteligencia artificial dando clic aquí
Objetivos
- se espere que al final de la clase el alumno logre conocer y entender los métodos para resolver un sistema de ecuaciones, además que pueda lograr aplicar los métodos enseñados en la resolución de diversos ejercicios , para de este modo poder resolver de forma óptima un sistema de ecuaciones lineales de 2 incognitas.
Recursos
mira el siguiente idea para que te hagas una idea de lo que veremos
https://www.youtube.com/watch?v=0mHCQYQGu04
analiza las siguientes imágenes y encuentra las coordenadas del punto de intersección de estas

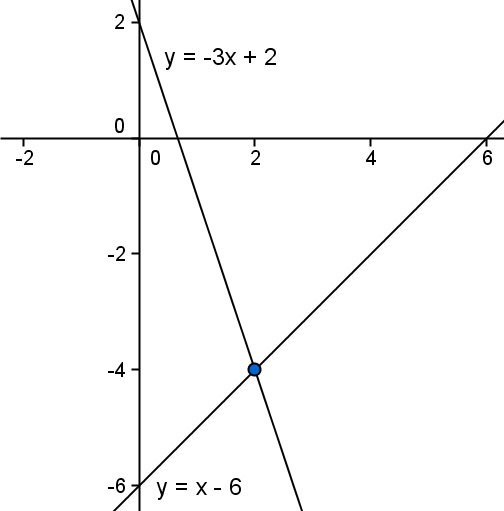
geogebra
ingresa al siguiente links, en el cual tendrás que ingresar 2 ecuaciones lineales y veras si estas se intersectan en algún punto.
Requisitos
- conocimiento básico de álgebra
- conocimiento del geogebra
- saber resolver ecuaciones lineales
- manejo básico del computador
Proceso
en la primera sesión, será teórica, es decir el profesor lo que hará será enseñarles a los alumnos cada uno de los métodos que existen para poder resolver un sistema de ecuaciones con dos incógnitas.
objetivos de aprendizaje:
conocer y entender los métodos para resolver un sistema de ecuaciones
Definir Actividad 2
el fin de esta sesión es que comprobar si es que los estudiantes lograron entender los métodos de resolución de ecuaciones lineales, para lo cual se le presentaran una serie de ejercicios resueltos y otros que tendrá que resolver.
objetivo de aprendizaje:
resolver sistemas de educaciones lineales, haciendo uso de algunos de los métodos enseñados.
Actividades Docente
el docente explicará cada uno de los métodos que se pueden utilizar para dar solución a un sistema de ecuaciones.
Llamamos sistema de ecuaciones a un conjunto cualquiera de ecuaciones. Por ejemplo, las ecuaciones:
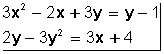
forman un sistema de dos ecuaciones con dos incógnitas.
El conjunto de ecuaciones:
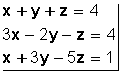
forman un sistema de tres ecuaciones con tres incógnitas.
Se llama grado del sistema de ecuaciones al mayor exponente al que se encuentre elevada alguna incógnita del sistema.
Por ejemplo,
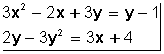
es un sistema de dos ecuaciones con dos incógnitas de segundo grado, porque el mayor exponente es 2 (la x e y al cuadrado). Este sistema con ecuaciones de segundo grado se llaman también sistema de ecuaciones cuadráticas.
El sistema de ecuaciones ![]() es de primer grado con dos incógnitas (porque todos los valores están elevados a 1, que no se escribe).
es de primer grado con dos incógnitas (porque todos los valores están elevados a 1, que no se escribe).
Cuando el sistema de ecuaciones es de primer grado y además no aparecen términos con las incógnitas multiplicadas entre sí(tipo x • y) se dice que es un sistema de ecuaciones lineales.
Resolviendo sistemas
Para resolver un sistema de ecuaciones existen los siguientes métodos:
Método de sustitución
Lo que debemos hacer:
1.- Despejar una de las incógnitas en una de las ecuaciones.
2.- Sustituir la expresión obtenida en la otra ecuación.
3.- Resolver la ecuación resultante.
4.- Calcular la otra incógnita en la ecuación despejada.
Ejemplo:
Resolver
![]()
Se despeja x en la segunda ecuación:
x = 8 – 2y
Se sustituyen en la primera ecuación:
3(8 – 2y) – 4y = – 6
Operando:
24 − 6y − 4y = − 6
24 – 10y = – 6
− 10y = − 6 − 24
− 10y = − 30
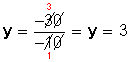
Se resuelve:
y = 3
Se sustituye este valor en la segunda:
x + 2(3) = 8
x + 6 = 8
x = 8 – 6 = 2
Solución del sistema:
x = 2, y = 3
Método de reducción
Lo que debemos hacer:
1.- Se igualan los coeficientes de una incógnita, salvo el signo, eligiendo un múltiplo común de ambos.
2.- Puede ser el producto de los coeficientes de esa incógnita.
3.- Se suman o restan, según convenga, las ecuaciones.
4.- Se resuelve la ecuación de primer grado resultante.
5.- Se calcula la otra incógnita sustituyendo el valor obtenido en una de las ecuaciones del sistema.
Ejemplo:
Resolver
![]()
Primero se deben igualar el 6 y el 8 de la incógnita x. Para hacerlo, amplificamos la primera ecuación por 4 y amplificamos la segunda ecuación por –3. Esto porque al multiplicar 6x por 4 queda 24x; y al multiplicar 8x por –3 queda –24x, y se anulan entre sí; o sea, hemos eliminado una incógnita para trabajar solo con la otra (la y). Luego hacemos lo mismo con la y.
|
|
Se elimina la y:
|
Método de igualación
Lo que debemos hacer:
1.- Se despeja una de las incógnitas en ambas ecuaciones.
2.- Se igualan las expresiones, con lo que obtenemos una ecuación con una incógnita.
3.- Se resuelve la ecuación resultante.
4.- El valor obtenido se sustituye en cualquiera de las dos expresiones en las que aparecía despejada la otra incógnita.
5.- Los dos valores obtenidos constituyen la solución del sistema.
Ejemplo:
Resolver
![]()
Despejamos x en la primera ecuación:

Despejamos x en la segunda ecuación:
x = –1 – 2y
Igualamos ambas expresiones:
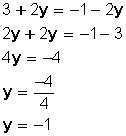
:Se sustituye este valor en la primera o segunda ecuación:
x = 3 + 2(−1)
x = 3 − 2
x = 1
Solución del sistema:
x = 1, y = –1
Otro ejemplo:
Resolver, por el método de igualación, el sistema
![]()
Despejamos, por ejemplo, la incógnita x de la primera y segunda ecuación:
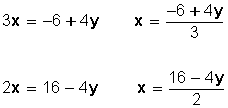
Igualamos ambas expresiones:
![]()
Luego, resolvemos la ecuación:
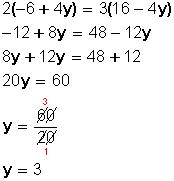
Sustituimos el valor de y, en una de las dos expresiones en las que tenemos despejada la x:
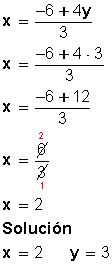
en esta sesión el docente pasa prácticamente a segundo plano, pues en esta sesión el alumno debe mostrar que aprendió lo que se le enseño en la sesión 2, por lo cuál el docente esta de apoyo ante dudas que pudiesen aparecer en los alumnos a medida que se va a vanzando.
Actividades Estudiante
el estudiante deberá leer y entender la materia y si no la entiende revisar los links
Resolviendo sistemas
Para resolver un sistema de ecuaciones existen los siguientes métodos:
Método de sustitución
Lo que debemos hacer:
1.- Despejar una de las incógnitas en una de las ecuaciones.
2.- Sustituir la expresión obtenida en la otra ecuación.
3.- Resolver la ecuación resultante.
4.- Calcular la otra incógnita en la ecuación despejada.
Ejemplo:
Resolver
![]()
Se despeja x en la segunda ecuación:
x = 8 – 2y
Se sustituyen en la primera ecuación:
3(8 – 2y) – 4y = – 6
Operando:
24 − 6y − 4y = − 6
24 – 10y = – 6
− 10y = − 6 − 24
− 10y = − 30
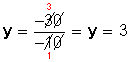
Se resuelve:
y = 3
Se sustituye este valor en la segunda:
x + 2(3) = 8
x + 6 = 8
x = 8 – 6 = 2
Solución del sistema:
x = 2, y = 3
Método de reducción
Lo que debemos hacer:
1.- Se igualan los coeficientes de una incógnita, salvo el signo, eligiendo un múltiplo común de ambos.
2.- Puede ser el producto de los coeficientes de esa incógnita.
3.- Se suman o restan, según convenga, las ecuaciones.
4.- Se resuelve la ecuación de primer grado resultante.
5.- Se calcula la otra incógnita sustituyendo el valor obtenido en una de las ecuaciones del sistema.
Ejemplo:
Resolver
![]()
Primero se deben igualar el 6 y el 8 de la incógnita x. Para hacerlo, amplificamos la primera ecuación por 4 y amplificamos la segunda ecuación por –3. Esto porque al multiplicar 6x por 4 queda 24x; y al multiplicar 8x por –3 queda –24x, y se anulan entre sí; o sea, hemos eliminado una incógnita para trabajar solo con la otra (la y). Luego hacemos lo mismo con la y.
|
|
Se elimina la y:
|
Método de igualación
Lo que debemos hacer:
1.- Se despeja una de las incógnitas en ambas ecuaciones.
2.- Se igualan las expresiones, con lo que obtenemos una ecuación con una incógnita.
3.- Se resuelve la ecuación resultante.
4.- El valor obtenido se sustituye en cualquiera de las dos expresiones en las que aparecía despejada la otra incógnita.
5.- Los dos valores obtenidos constituyen la solución del sistema.
Ejemplo:
Resolver
![]()
Despejamos x en la primera ecuación:

Despejamos x en la segunda ecuación:
x = –1 – 2y
Igualamos ambas expresiones:
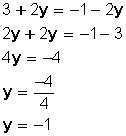
:Se sustituye este valor en la primera o segunda ecuación:
x = 3 + 2(−1)
x = 3 − 2
x = 1
Solución del sistema:
x = 1, y = –1
Otro ejemplo:
Resolver, por el método de igualación, el sistema
![]()
Despejamos, por ejemplo, la incógnita x de la primera y segunda ecuación:
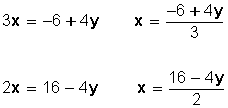
Igualamos ambas expresiones:
![]()
Luego, resolvemos la ecuación:
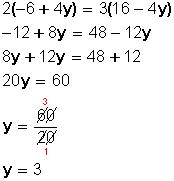
Sustituimos el valor de y, en una de las dos expresiones en las que tenemos despejada la x:
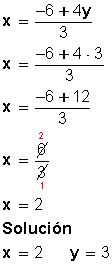
el primer paso a realizar será ver los ejercicios propuestos, para lo cual deberá ingresar a links que se entrega continuación.
http://http://www.educaplay.com/es/recursoseducativos/2201763/sistema_de_ecuaciones__d_.htm
posteriormente deberá ingresar al links que se entrega y resolver los ejercicios planteados-
http://www.educaplay.com/es/recursoseducativos/1968801/resuelve_las_ec.htm
Evaluación
en esta parte el estudiante deberá haber revisado todo lo anterior, por lo cual responderá a 5 preguntas con las cuales se vera si logro los aprendizajes esperados o no, para lo cual deberá ingresar al siguiente links.
http://www.educaplay.com/es/recursoseducativos/1968801/resuelve_las_ec.htm
Notas
http://www.educaplay.com/es/recursoseducativos/2201707/resuelve_la_sgte_eval_de_sist.htm
http://www.educaplay.com/es/recursoseducativos/2201763/sistema_de_ecuaciones__d_.htm
http://www.educaplay.com/es/recursoseducativos/2201765/resuelve_las_ec__d_.htm
Creditos
Proyecto Creado Por Karen Vergara Cardenas - Utilizando A Eduteka.org

*Nota: toda la información que aparece en los Proyectos de Clase y WebQuest del portal educativo Eduteka es creada por los usuarios del portal.