Inicio Actividades Otra Regresión
Regresión
Regresión
¿En qué consiste la actividad Regresión ?
Correlación y regresión son indicadores utilizados frecuentemente en estadística. La correlación se usa para ver si existe relación entre dos variables y para responder preguntas como estas: ¿Cree usted que existe alguna relación entre:
- El tiempo que pasa estudiando para un examen y la calificación que obtiene?
- El tiempo que dedica un equipo a entrenar y el número de victorias que logran en una temporada?
- su estatura y su peso?
- la clase de zapatos que usa y qué tan rápido puede correr?
Si se establece alguna relación como las anteriores, entonces se puede usar la correlación para determinar qué tan fuerte es tal relación. Una vez descubierta una correlación, se usa la regresión para encontrar la ecuación que relaciona las dos variables. Esta ecuación puede mostrar si las dos variables se relacionan positiva o negativamente.
Recursos para la clase
- Actividad Regresión lineal múltiple
- Actividad Gráfico de dispersión
- Discusión sobre Relaciones de datos bivariados
- Discusión sobre Coeficientes de correlación
- Discusión sobre Hallar residuos
- Discusión sobre Graficar e interpretar datos bivariados
- Discusión sobre Variables independientes y dependientes
- Discusión sobre Recta de mejor ajuste
- Discusión sobreValores atípicos
- Discusión sobre Datos univariados y datos bivariados
- Discusión sobre El uso de residuos para identificar una recta de mejor ajusta
- Taller Preguntas de exploración sobre Regresión
- Taller Preguntas de exploración sobre Regresión(doc)
Actividad
¿Cómo puedo utilizar esta actividad?
Descripción
La aplicación sobre regresión permite que el usuario grafique un conjuntos de datos bivariados, determine la recta de mejor ajuste para los datos y verifique la precisión de la recta de mejor ajuste.
Controles y Resultados
- Primero, el usuario necesita ingresar los datos. Esto puede hacerse de dos maneras:
- Digitando las coordenadas en la caja de datos y presionando después el botón Actualizar Gráfica
Si tiene dificultades copiando los datos de la aplicación y pegándolos en una hoja de Excel, consulte, por favor, nuestra Ayuda Copiar/Pegar de Excel - El usuario puede graficar puntos en la cuadrícula seleccionando el botón Añadir Puntos, poniendo el ratón sobre la posición deseada de la cuadrícula, haciendo click y repitiendo el proceso con cada uno de los puntos en la lista de datos.

- Digitando las coordenadas en la caja de datos y presionando después el botón Actualizar Gráfica
- Cuando el usuario finalice el ingreso de datos, puede ensayar a crear una línea de mejor ajuste, seleccionando la opción Ajustar tu propia recta

- Una vez seleccionada la opción Ajustar tu propia recta aparecerá en la cuadrícula una recta de color verde. El usuario puede moverla seleccionando el botón Mover la curva de ajuste haciendo click en los círculos verdes y arrastrándolos hasta la posición deseada.

- El usuario puede verificar la exactitud de su recta de ajuste, seleccionando la opción Mostrar la recta de mejor ajuste

- r es el coeficiente de correlación lineal. r describe la fuerza de la relación lineal. r es un número entre -1 y 1. Si r= 0 entonces no hay relacion entre los datos. Si r es positivo, los datos tienen una correlación positiva; si r is negativo, los datos tienen una correlación negativa. Entre más cercano a 1 esté el valor de r, más fuerte es la correlación positivia; entre más cerca de -1 esté el valor de r, más fuerte es la correlación negativa.
- Y denota la ecuación de la recta
- El usuario puede eliminar puntos bien sea borrándolos de la tabla de datos o presionando el botón Actualizar Gráfica o seleccionando el cuadro Eliminar Puntos y haciendo click en los puntos que se desea eliminar de la cuadrícula.

El usuario puede mover puntos seleccionando el ítem Mover Puntos, haciendo click y arrastrando el punto que se quiere mover hasta la posición deseada.. 
- Botones Zoom/Desplazamiento. En la esquina superior derecha del gráfico hay tres botones con imágenes de lupas. De arriba a abajo, representan acercamiento, alejamiento y desplazamiento, respectivamente.
-
Para un zoom de acercamiento haga click en el botón superior para activarlo y después haga click y arrastre sobre el área de la gráfica que se quiere magnificar. Las imágenes siguientes muestran la preimagen a medida que el usuario arrastra sobre el área a magnificar y la imagen magnificada. Observe que despues de hacer click y arrastrar sobre el área seleccionada el botón ya no se ve seleccionado.
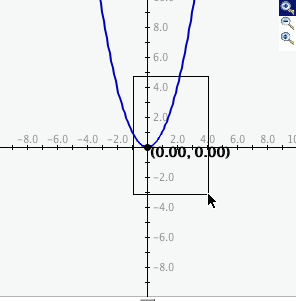
- Para disminuir el zoom, simplemente active el botón del medio. La gráfica se disminuirá automáticamente al duplicarse los valores máximo y mínimo de los ejes.
- Para usar la funcion de desplazamiento, haga click en el tercer boton para activarlo. Haga click y arrastre sobre la gráfica y se obtendrá el desplazamiento conforme al movimiento del ratón. Al aflojar la presión sobre el ratón se libera también el botón de desplazamiento.
- El usuario puede mostrar los residuos activando el botón Mostrar Residuos
- Cuando se selecciona el botón Mostrar Residuos, aparece una pantalla de residuos. En la primera columna de la tabla está la coordenada x de cada uno de los puntos ingresados. En la segunda columna están los residuos de su recta. Y en la tercera columna están los residuos de la recta de mejor ajuste. Situada en la base de la pantalla de residuos hay una Gráfica de Residuos. Si la opción Mostrar la recta de mejor ajuste ha sido seleccionada, aparecerán puntos rojos en la gráfica; si la opción Ajustar tu propia recta ha sido seleccionada, aparecerán puntos verdes en la gráfica; Si ambas opciones han sido seleccionadas, aparecerán puntos rojos y verdes en la gráfica. Esta gráfica ilustra la distancia entre las rectas de mejor ajuste y el conjunto dado de puntos.

El usuario puede retornar la gráfica a su estado original activando el botón Restablecer, situado en la parte inferior derecha de la pantalla.
Recursos y contexto curricular
La aplicación sobre regresión se ha desarrollado para que el usuario pueda graficar un conjunto de datos bivariados, determinar la recta de mejor ajuste para los datos y chequear la precisión de su recta de mejor ajuste. Esta actividad determina el coeficiente de correlación, r, para las rectas de mejor ajuste e introduce a los estudiantes en el tema de residuos. Trabajar la actividad en grupos de dos o tres estudiantes durante 10-15 minutos da buenos resultados.
Ubicación en el currículo de matemáticas
- Enseñar a los estudiantes cómo influyen los datos en la recta de mejor ajuste.
- Diseñar prácticas para que los estudiantes determinen la recta de mejor ajuste para un conjunto de datos.
- Inicar a los estudiantes en el tema de residuos.
- Permitir que los estudiantes exploren con el coeficiente de correlación, r.
Estándares alcanzados
Grados 6-8
- Álgebra
- Usar modelos matemáticos pra representar y comprender relaciones cuantitativas.
- Análisis de datos y probabilidad
- Desarrollar y evaluar inferencias y predicciones basadas en datos.
- Formular preguntas que puedan abordarse con datos y recopilar, organizar y representar datos relevantes para responderlas.
- Seleccionar y usar métodos estadísticos apropiados para el análisis de datos.
Grados 9-12
- Álgebra
- Analizar el cambio en diferentes contextos.
- Representar y analizar situaciones y estructuras matemáticas utilizando simbolos algebraicos.
- Entender patrones, relaciones y funciones.
- Utilizar modelos matemáticos para representar y comprender relaciones cuantitativas.
- Análisis de datos y probabilidad
- Formular preguntas que puedan abordarse con datos y recopilar, organizar y representar datos relevantes para responderlas.
- Seleccionar y usar métodos estadísticos apropiados para el análisis de datos.
Esté preparado para:
- correlación.
- residuos.
- cómo interpreetar la tabla y gráfico de residuos
- el coeficiente de correlación lineal, r.
- variables independientes y dependientes.
Recursos para clases
- Actividad Regresión lineal múltiple
- Actividad Gráfico de dispersión
- Discusión sobre Relaciones de datos bivariados
- Discusión sobre Coeficientes de correlación
- Discusión sobre Hallar residuos
- Discusión sobre Graficar e interpretar datos bivariados
- Discusión sobre Variables independientes y dependientes
- Discusión sobre Recta de mejor ajuste
- Discusión sobreValores atípicos
- Discusión sobre Datos univariados y datos bivariados
- Discusión sobre El uso de residuos para identificar una recta de mejor ajusta
- Lección sobre Regresión lineal y Correlación
- Lección sobre Datos univariados y bivariados
- Taller Preguntas de exploración sobre Regresión
- Taller Preguntas de exploración sobre Regresión(doc)
