Inicio Actividades Otra Rotación de funciones
Rotación de funciones
Rotación de funciones
¿En qué consiste la actividad Rotación de funciones ?
Esta actividad permite la creación de sólidos tridimensionales rotando las gráficas de funciones alrededor de un eje horizontal o uno vertical. A continuación la aplicación calcula el volumen y el área de la superficie del sólido creado. Esto permite que el usuario practique integración, utilizada en la fórmula para el cálculo del volúmen y del área de la superficie de sólidos generados por rotación.
El usuario puede decidir si la rotación se hace alrededor de una recta horizontal o de una recta vertical. Si es alrededor de una recta horizontal, las ecuaciones deben estar en función de x (por ejemplo, f(x)= x+3). Si la rotación es alrededor de un eje vertical, las ecuaciones deben estar en función de y ( por ejemplo, f(y)=y-2). Esto es necesario para la integración.
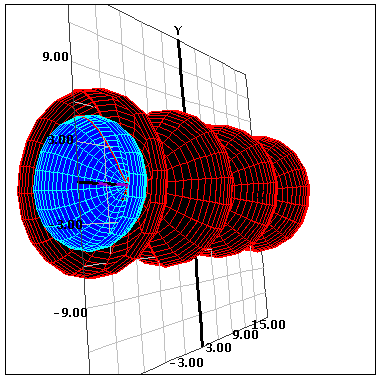
Cuando se rota alrededor de un eje, pueden suceder dos cosas: Si es sólo una función que se rota alrededor de un eje, se forma un sólido. A continuación se ve un ejemplo de una función rotada alrededor de un eje para crear un sólido.
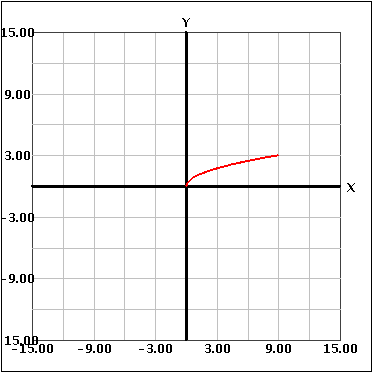
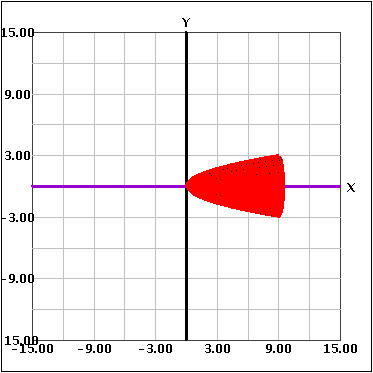
La otra situación se presenta cuando se rotan dos funciones alrededor de un eje. Esto crea una figura "hueca" porque se rota el área comprendida entre las curvas alrededor de los ejes, como se ve a continuación.
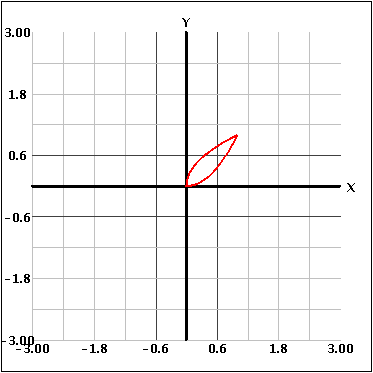
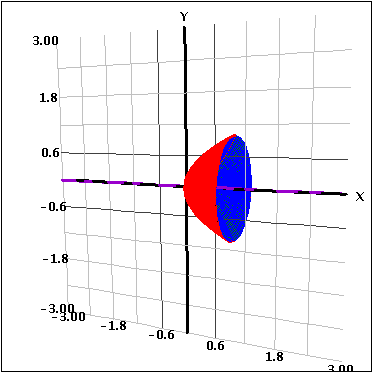
La actividad permite también restringir las fronteras de las funciones. Esto hace que el usuario pueda considerar una sección de las funciones comprendida entre intersecciones. pudiendo así considerar una sección de las funciones entre intersecciones. Entonces, para calcular el volumen total, el usuario puede combinar las diferentes secciones.
Recursos para la clase
- Acitividad Transmógrafo 3D
- Acitividad Integrar
- Actividad Folleto de datos de multi-funciones
- Taller Rotación de funciones Preguntas de exploración
- Taller Rotación de funciones Preguntas de exploración (doc)
Actividad
¿Cómo puedo utilizar esta actividad?
Descripción
Esta actividad permite hallar el volumen y el área generados por la rotación de funciones alrededor de los ejes. La aplicación puede utilizarse para practicar calculando integrales y usando los métodos de estimación de disco y arandela.
Controles y Resultados
Para graficar y rotar una o dos funciones, decida primero si la rotación será alrededor de un eje vertical o no vertical. Puede especificar el eje de rotación escribiendo un número en el cuadro etiquetado como " a través de y =" o "a través de x =".
- Entonces, ingrese las funciones en los cuadros etiquetados "Función 1" y "Función 2"

- Para cambiar los valores de x en los cuales se evalúa la función, cambie los valores en los cuadros rectángulos "desde" y "hasta".

- Cuando haya terminado, presione el botón "Definir funciones", para graficar la(s) funcion(es).

Ahora puede girar la o las funciones alrededor de un eje.
- Para modificar la velocidad de rotación, haga click en el menú desplegable y elija entre Rápida, Mediana y Lenta.
- Finalmente, haga click en "Rotar", para rotar la (o las) función(es) alrededor del eje escogido.
- Despues de girar las funciones, usted puede hacer click y arrastrar en cualquier punto de la gráfica para ver las funciones en 3 dimensiones. También puede hacer click en "Restablecer vista" para regresar a la orientación predeterminada de la vista.

(Restablecer vista)
- Cuando las funciones han sido rotadas, se mostrarán el volumen y el área de la superficie en el cuadro "Estadisticas".
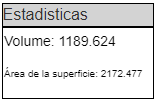
Cuando las funciones han sido rotadas, usted puede cambiarles el color y decidir si se muestran como sólidos o como armazón en alambre.
- Para alternar entre representación como sólido o como estructura, seleccione los botones "-Sólido" o "Armazón " en la parte superior de la aplicación.
- El modo Armazón muestra la función como contornos lineales a través de los cuales se puede ver.
- El modo Sólido, llena el armazón con otro color, "renderizando" las funciones más como objetos, de tal manera que uno no puede ver a través de ellas.

- Para cambiar el color de las funciones utilice el menú desplegable de la derecha
- Tenga en cuenta que sólo se puede definir un color para cada función en el modo Armazón, pero pueden fijarse un color para el "cableado" y otro para el "relleno" en el modo armazón.
Para cambiar las dimensiones del gráfico desplegado presione en "Definir Ventana". Funciones cuyos valores excedan 3 veces la dimensión de la gráfica mostrada (la "Ventana") no se muestran más allá de ese punto. Al agrandar la ventana se puede ver la función graficada completa. Por ejemplo, la función x^2 toma el valor 225 en x=15, pero un diagrama en el que las líneas de la cuadrícula sólo llegan hasta 15 no permitirá graficar la función más allá del valor 45; esto puede remediarse escogiendo ymax= 80.
- Aparecerá un campo emergente que le permitirá definir las dimensiones de los ejes x, y.
Si en algún momento usted quiere abandonar la función que está siendo graficada, simplemente use el botón "Borrar Gráfica".
Recursos y contexto curricular
Esta aplicación es una versión ampliada de Transmógrafo 3D. Este modelo tridimensional permite explorar funciones y sus rotaciones alrededor de un eje. Después de que una o dos funciones han sido rotadas, la aplicación calcula el área de la superficie y el volumen del sólido resultante. Seleccionando y arrastrando el gráfico, los usuarios pueden cambiar el punto desde el cual se ve el gráfico, para comprender mejor las funciones, la rotación y sólido resultante.
Ubicación en el currículo de matemáticas
Esta actividad puede usarse para:
- Explorar volúmenes y área de la superficie de sólidos particulares.
- Hacer una introducción al tema de cálculo de volúmenes y áreas de superficies mediante integración
- Practicar la solución de integrales que corresponden a volúmenes y áreas de superficies.
- Visualizar la rotación de una función o de un par de funciones.
Estándares alcanzados
Grados 8-12
- Cálculo
- Los estudiantes usan integrales para resolver problemas de áreas, velocidad, aceleración, volumen de un sólido, área de una superficie de revolución, longitud de una curva y trabajo.
- Los estudiantes calculan, manualmente, las integrales de una amplia variedad de funciones utilizando técnicas de integración tales como sustitución, integración por partes y sustitución trigonométrica. También pueden combinar estas técnicas cuando sea apropiado hacerlo.
Esté preparado para:
- Explicar cómo la integración se relaciona con el volumen y el área de la superfice de sólidos rotados.
- Describir los métodos de disco y arandelas para el cálculo de volúmenes.
- Describe el método shell para calcular áreas de superficies.
- Explicar cómo dx y dy se factorizan en el cálculo de áreas y volúmenes.
Recursos para clases
- Acitividad Transmógrafo 3D
- Acitividad Integrar
- Actividad Folleto de datos de multi-funciones
- Taller Rotación de funciones Preguntas de exploración
- Taller Rotación de funciones Preguntas de exploración (doc)
