Area y Asignatura

Matemáticas - Aritmética

Edad

• No hay restriccion de edad

Herramientas

• Cómics
• Imágenes
• Video
• Libros Digitales

Objetivos

---

Objetivo general

Aplicar con habilidad las propiedades basicas de los numeros complejos para enfrentar diversas situaciones problema que no son posibles de abordar por medio de numeros reales.

---

Objetivos especificos

1. Efectuar con destreza operaciones algebraicas entre numeros complejos.

 2. Representar geometricamente numeros complejos en el plano y sus propiedades.

---

 

Recursos

Requisitos

Para este tema se se requiere  conocimiento previo de numeros naturales, enteros, racionales, irracionales, reales y propiedades de los exponentes.  Partiremos del nivel más básico posible e iremos avanzando poco a poco hasta adquirir los conocimientos necesarios para poder trabajar con números complejos.

En el momento en que aparezca alguna expresión más compleja será explicada minuciosamente para que no tengas dificultad alguna en ella.

Este curso está dirigido a todos aquellos alumnos que deseen comenzar a formarse en el estudio de los números complejos.

Proceso

El propósito de esta actividad es que los alumnos  interpreten la importancia de conocer el conjunto numérico: Números Complejos. Que descubran que con ellos se pueden resolver situaciones que con otros conjuntos numéricos no es posible. A la vez, que investiguen también sus aplicaciones en las distintas áreas.

Actividades Docente

para el desarrolo de esta tematica se hara la respectiva explicacion utilizando varios ejemplos

Definición y operaciones de números complejos en forma binómica

Tabla de contenidos 

Definición de número complejo

Un número complejo zz se define como un par ordenado de 

z=(a,b)cona,b∈Rz=(a,b)cona,b∈R

donde el primer elemento del par ordenado se llama parte real del número complejo, y el segundo elemento se llama parte imaginaria:

Re(z)=aRe(z)=a

Im(z)=bIm(z)=b

En los números complejos se definen las siguientes operaciones:

(a,b)+(c,d)=(a+c,b+d)(a,b)+(c,d)=(a+c,b+d)

(a,b).(c,d)=(ac–bd,ad+bc)(a,b).(c,d)=(ac–bd,ad+bc)

Con estas operaciones, puede demostrarse que el conjunto de los números complejos tiene las mismas propiedades que los reales con la suma y el producto. No nos extenderemos desarrollando esta cuestión algebraica porque en la práctica lo usual es operar con otras expresiones de los números complejos, como veremos a continuación.

Podemos identificar de manera natural los complejos de parte imaginaria nula con los números reales:

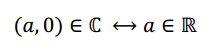
Por otra parte, los números de parte real nula: z=(0,b)z=(0,b) se denominan imaginarios puros. Se define la unidad imaginaria:

i=(0,1)unidadimaginariai=(0,1)unidadimaginaria

Podemos entonces deducir otra forma de expresar un número complejo:

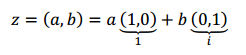
z=a+biformabinómicaz=a+biformabinómica

Observación: en algunos textos de Física y de Ingeniería la unidad imaginaria se designa como jj , para no confundir con la ii que suele indicar la intensidad de corriente eléctrica.

Dado que hemos definido un número complejo como un par ordenado de números reales, es natural interpretarlo como un punto del plano. En el eje de abscisas (eje real) ubicaremos los complejos de parte imaginaria nula. Y en el eje de ordenadas (eje imaginario) ubicaremos los imaginarios puros:

Operaciones en forma binómica

Suma y resta

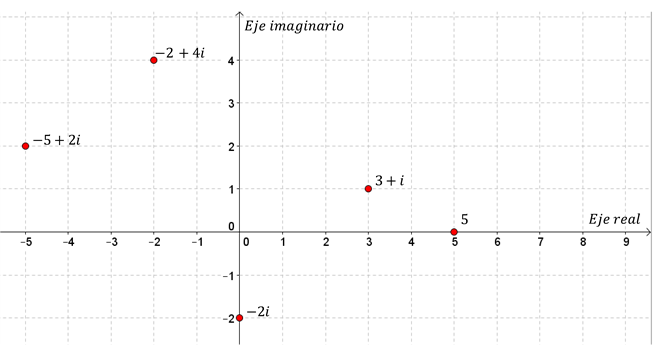
Si z1=a+biz1=a+bi y z2=c+diz2=c+di, entonces:

z1+z2=(a+bi)+(c+di)=(a+c)+(b+d)iz1+z2=(a+bi)+(c+di)=(a+c)+(b+d)i

Análogamente: z1–z2=(a–c)+(b–d)iz1–z2=(a–c)+(b–d)i

Multiplicación

    z1.z2=(a+bi).(c+di)=ac+adi+bic+bdi2[1]z1.z2=(a+bi).(c+di)=ac+adi+bic+bdi2[1]

¿Cuánto vale i2i2?

De acuerdo con la multiplicación definida:
(a,b).(c,d)=(ac–bd,ad+bc)[2](a,b).(c,d)=(ac–bd,ad+bc)[2]

Para i=(0,1)i=(0,1) resulta:

i2=(0,1).(0,1)=(–1,0)i2=(0,1).(0,1)=(–1,0)que identificamos con el número real (–1)(–1).

En resumen:

i2=–1i2=–1

Reemplazando en [1][1] resulta:

z1.z2=(ac–bd)+i(ad+bc)z1.z2=(ac–bd)+i(ad+bc)

Pueden verificar que es coherente con la definición [2][2].

Conjugado de un número complejo

El conjugado de z=a+biz=a+bi , se define así:

¯z=a–biz¯=a–bi

Observamos que zz y ¯zz¯ son simétricos respecto del eje real, como muestra la siguiente figura:

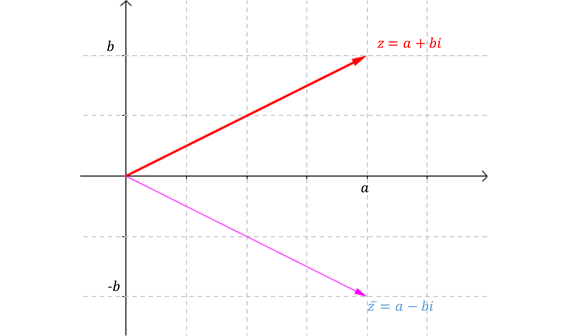
Propiedades:

1) z+¯z=a+bi+a–bi=2a=2Re(z)z+z¯=a+bi+a–bi=2a=2Re(z)

2) z–¯z=a+bi–(a–bi)=2bi=2i.Im(z)z–z¯=a+bi–(a–bi)=2bi=2i.Im(z)(recordar que Im(z)∈RIm(z)∈R )

3) z.¯z=(a+bi)(a–bi)=a2–abi+bia–b2i2=(a2+b2)∈R>0z.z¯=(a+bi)(a–bi)=a2–abi+bia–b2i2=(a2+b2)∈R>0para todo z≠0z≠0

División en complejos

Esta última propiedad nos permite calcular el cociente entre dos números complejos.

Sean z1=a+biz1=a+bi , z2=c+diz2=c+di

Para hallarz1/z2z1/z2multiplicamos el numerador y el denominador por el conjugado del denominador:

z1z2=z1z2.¯¯¯¯¯z2¯¯¯¯¯z2z1z2=z1z2.z2¯z2¯

Entonces:

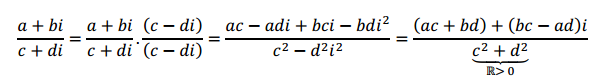
Ejemplos

Sean los números complejos:
    z1=2+3i;z2=1–i;z3=–3+i;z4=1–iz1=2+3i;z2=1–i;z3=–3+i;z4=1–i

Calcular:

 Resolución

Ítem a

z1–2z2=(2+3i)–2(1–i)=2–2+i(3+2)=5iz1–2z2=(2+3i)–2(1–i)=2–2+i(3+2)=5i

Ítem b

z1.z3=(2+3i)(–3+i)=–6+2i–9i+3i2=–9–7iz1.z3=(2+3i)(–3+i)=–6+2i–9i+3i2=–9–7i

Ítem c

z22+z3=(1–i)2+(–3+i)=1–2i+i2–3+i=–3–iz22+z3=(1–i)2+(–3+i)=1–2i+i2–3+i=–3–i

Ítem d

z4z3=1–i–3+i=1–i–3+i.(–3–i)(–3–i)=–3+3i–i+i29–i2=–4+2i10=–25+15iz4z3=1–i–3+i=1–i–3+i.(–3–i)(–3–i)=–3+3i–i+i29–i2=–4+2i10=–25+15i

Ítem e

z1z4=2+3i1–i.1+i1+i=–12+52iz1z4=2+3i1–i.1+i1+i=–12+52i

Potencias de ii

Las potencias de la unidad imaginaria tienen un comportamiento cíclico, como veremos a continuación:

i0=1i0=1

i1=ii1=i

i2=–1i2=–1

i3=i2.i=–ii3=i2.i=–i

i4=i3.i=1i4=i3.i=1

i5=i4.i=ii5=i4.i=i

Y así sucesivamente.

¿Cómo podemos determinar cualquier potencia de ii , por ejemplo i514i514 ? Dividiendo el exponente por 4, se obtiene: 514=128.4+2514=128.4+2

Entonces resulta:

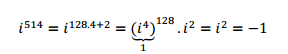
O sea que: i514=i2i514=i2 , siendo 22 el resto de dividir 514 por 4.

En resumen:

in=irin=ir , siendo rr el resto de la división de nn por 4 (n∈Nn∈N)

https://aga.frba.utn.edu.ar/definicion-y-operaciones-de-numeros-complejos-en-forma-binomica/

 

Actividades Estudiante

Actividad del estudiante

http://mestreacasa.gva.es/c/document_library/get_file?folderId=500013956017&name=DLFE-796924.pdf

Evaluación

El estudiate para poder aprobar este tema tendra que resolver este cuestionario

http://file:///C:/Users/DaNiELiTa/Downloads/Examen-de-n%C3%BAmeros-complejos.pdf

Notas

El estudiate si reponde 10 de 15 su nota sera 3.5

el estudiante si responde 13 de 15 su nota es 4

Créditos