El caso de la geometría y la visualización

https://eduteka.icesi.edu.co/articulos/GeometriaVisual

COGNICION Y COMPUTACION
EL CASO DE LA GEOMETRIA Y LA VISUALIZACION

Por Luis Moreno Armella [2]
Matemática Educativa, Cinvestav.

USO DE LAS CALCULADORAS GRÁFICAS Y ALGEBRAICAS

El Ministerio de Educación Nacional de Colombia (MEN) inició en el año 2000 la fase piloto del proyecto de Incorporación de Nuevas Tecnologías al Currículo de Matemáticas [1]. En esta etapa se trabajó en 44 colegios de Educación Básica Secundaria y Media y 16 Escuelas Normales Superiores. El objetivo consistió en mejorar el aprendizaje de las matemáticas mediante la utilización en el aula de calculadoras gráficas y algebraicas [2].

El proyecto estuvo a cargo de educadores matemáticos del MEN con la asesoría de Luis Moreno Armella [3] del CINVESTAV de México. Se conformaron equipos regionales comprometidos con la diseminación de la cultura informática en la educación; se implementó un programa para desarrollar en los docentes las competencias tecnológicas necesarias para el proyecto; y se produjeron materiales de apoyo para integrar el uso de calculadoras gráficas y algebraicas [4] en diferentes aspectos del currículo.

Fruto de esta última iniciativa fue la recopilación de algunos materiales importantes que marcaron el desarrollo de la fase piloto del proyecto y que fueron publicados bajo el título “Memorias del Seminario Nacional de Docentes: Uso de Nuevas Tecnologías en el Aula de Matemáticas” [5]. Del primer capítulo de este libro tomamos el siguiente artículo por encontrar en él razones de peso para utilizar en el aula herramientas tecnológicas que permiten al estudiante manipular directamente (visualización e interacción) objetos geométricos para lograr una mayor comprensión.

GEOMETRÍA Y MODELOS COMPUTACIONALES

Si bien el impacto de las calculadoras y computadoras sobre las prácticas cotidianas no ha sido tan fuerte como se esperaba desde hace ya más de dos décadas, el impacto epistemológico ha sido mayor que lo previsible en ese entonces (Balacheff & Kaput, 1996). Esto se debe fundamentalmente al proceso de reificación de los objetos matemáticos y a las relaciones entre ellos que el estudiante puede activar en los entornos interactivos computacionales. Lo anterior permite una forma de actividad mucho más directa que la que era posible anteriormente. Este nuevo realismo matemático hace indispensable la extensión de la transposición didáctica a los contextos computacionales dando lugar a una transposición informática (Balacheff, 1994).

Los nuevos entornos promueven una transformación a nivel epistemológico de la experiencia matemática del estudiante.

Las situaciones de orden cognitivo y epistemológico a que nos hemos referido, encuentran como vehículos de expresión a los llamados micromundos computacionales (Balacheff & Kaput, 1996). En términos más precisos, podemos decir que un micromundo está compuesto de:

i) Un conjunto de objetos primitivos y operaciones que se realizan sobre estos objetos que permite la operación formal del micromundo.
ii) Un dominio fenomenológico, que relaciona los objetos y las operaciones con los fenómenos que podemos apreciar a nivel de la pantalla. Este dominio determina el tipo de retroalimentación que se produce como consecuencia de las acciones y decisiones que toma el estudiante durante la exploración.

Puesto que no están predeterminadas las acciones del estudiante, él podrá explorar la estructura de los objetos, relaciones y registros representacionales que le suministra el micromundo. Podrá incluso, generar nuevos objetos complejos a partir de los objetos primitivos originales. Desde esta perspectiva, podemos decir que el micromundo evoluciona a medida que crece el conocimiento del estudiante.

CABRI: UN MUNDO GEOMÉTRICO NUEVO

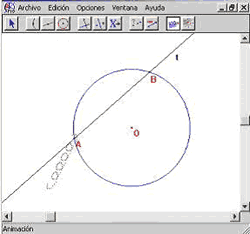
Señalaremos mediante un ejemplo, algunos de los problemas cognitivos que los nuevos recursos tecnológicos hacen explícitos: CABRI-GÉOMÈTRE. En dicho entorno computacional, uno puede manipular directamente las figuras construidos en la pantalla mediante el arrastre (drag) de ciertas partes de ellas. De hecho, una vez elaborada una figura geométrica, ella reconoce cuáles son las partes (de dicha figura) que pueden ser arrastradas. Es fundamental señalar que esto ocurre, sin alterar las relaciones estructurales entre las partes constitutivas de la figura. Por ejemplo, en la figura 1, se puede arrastrar el punto A hasta hacerlo coincidir con B. Durante el proceso, las relaciones estructurales (el que la recta t esté determinada por los puntos A y B, por ejemplo) no se alteran. Podemos exhibir entonces que la aproximación hacia B transformará a dicha recta en una recta tangente. El lector haría bien en procesar estos ejemplos en su computadora o calculadora (TI-92) pues nada sustituye a la dinámica que podemos apreciar en la pantalla. 

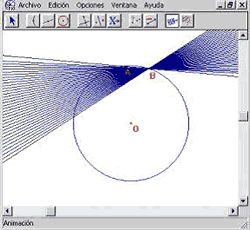Figura 1

LA VISUALIZACION EN LOS ENTORNOS COMPUTACIONALES

La visualización ha sido un tema estudiado intensamente por la didáctica, desde el arribo de las máquinas con capacidades de graficación a los sistemas educativos.

Cuando se explora un procedimiento escrito en un lenguaje computacional, por ejemplo en Logo, el estudiante experimenta las relaciones entre el código simbólico propio del lenguaje computacional y los fenómenos visuales que aparecen en la pantalla de la computadora. Por esta vía se puede lograr la extensión de la relación que la geometría analítica establece entre una ecuación y una curva del plano. Allí se va de la ecuación a la curva determinada por dicha ecuación; ahora, podemos invertir la correspondencia e ir de la figura al código. Es interesante observar que las soluciones simbólicas que pueden corresponder a una figura dada, son diversas. Ello abre una oportunidad para el aprendizaje ya que los alumnos pueden comparar las distintas soluciones a un mismo problema (encontrar un código que corresponda a una figura dada) y llegan al entendimiento que los problemas de matemáticas no tienen solución única y que la decisión sobre la elección de la mejor solución deberá hacerse sobre criterios que pueden discutirse en el salón de clases. La manipulación del entorno geométrico permite la ampliación de la experiencia posible del estudiante. Dado el control formal del entorno, las experiencias desarrolladas dentro del micromundo pueden considerarse como genuinas experiencias geométricas.

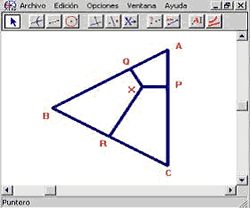
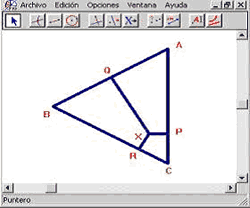
La visualización y las representaciones externas permiten atender otro problema medular del aprendizaje y de la enseñanza de las matemáticas. Nos referimos al problema de la validación de los enunciados matemáticos. Por ejemplo, consideremos la situación: se tiene un triángulo equilátero y se toma un punto cualquiera de su interior y desde allí se trazan las alturas a los lados del triángulo (ver figura 2).

Se pide a los estudiantes que traten de determinar el valor numérico de la suma de las tres alturas sabiendo que dicha suma es independiente de la elección del punto interior.

En CABRI GÉOMÈTRE, los estudiantes tienen la posibilidad de mover (drag) el punto en el interior del triángulo preservando, como ya hemos dicho, las relaciones estructurales de la construcción original. Por ello responde el código interno del CABRI. Entonces, bajo esta hipótesis, podemos manipular las construcciones geométricas seguros de que nuestras manipulaciones no cambiarán el dato numérico que estamos buscando. las exploraciones de los estudiantes los llevan finalmente a la siguiente conclusión: si la suma de distancias no cambia, entonces podemos desplazar el punto interior a un vértice del triángulo y hacer evidente que la suma de las distancias coincide con la altura del triángulo.

Lo anterior es un ejemplo de que la manipulación directa de los objetos geométricos hace posible la experimentación en dominios que anteriormente eran inaccesibles para el estudiante. Además, su conocimiento queda marcado por relación dialéctica entre percepción y conceptualización durante la interacción con la interfase del sistema.

MEDIACIÓN Y CONTEXTUALIDAD

Una característica del funcionamiento mental, tanto al nivel del individuo como al nivel interindividual, es que ese funcionamiento está mediado por instrumentos materiales y por instrumentos simbólicos. Estos últimos incluyen, por ejemplo, las diversas formas de lenguajes sociales, diagramas, y sistemas matemáticos.

Una tesis central sobre la cognición desde la perspectiva social (Wertsch, 1993) es que la presencia de los instrumentos de mediación transforma de raíz la actividad cognitiva del estudiante determinando así la estructura de una nueva acción instrumental. La situación es análoga a la que se tiene ante la presencia de una herramienta material vinculada a un proceso técnico.

Los medios computacionales conducen a una redefinición de las fronteras entre la acción individual y la acción social. El estudiante, auxiliado de sus instrumentos computacionales, construye una versión del conocimiento. El conocimiento y el aprendizaje son, por su naturaleza, situados. Es decir, dependen en su construcción y en su interpretación, de la especificidad del contexto en el que surgen. Por lo tanto, para que el estudiante pueda utilizar el conocimiento construido, en otros contextos, hace falta la intervención permanente del profesor quien a través de sus propuestas conduce al estudiante a una nueva construcción (que se da a un nuevo nivel de abstracción) del esquema cognitivo que subyace a su construcción situada.

REFERENCIAS

[1] Proyecto de Incorporación de Nuevas Tecnologías al Currículo de Matemáticas de la Educación Básica secundaria y Media de Colombia. Ministerio de Educación Nacional (MEN). Acastiblanco@mineducacion.gov.co, macosta@mineducacion.gov.co, Teléfono: (57 1) 222-2800 Ext 2111 o 2113.

[2] Conversación de EDUTEKA con la doctora Ana Celia Castiblanco Paiba, Coordinadora General del Proyecto de Incorporación de Nuevas Tecnologías al Currículo de Matemáticas en la Educación Básica secundaria y media en Colombia. 

[3] Luis Moreno Armella es investigador del Departamento de Matemática Educativa del Centro de Investigación y Estudios Avanzados de México-Cinvestav. Es asesor del proyecto de calculadoras del MEN. Ver otro artículo publicado en EDUTEKA de este autor: “Instrumentos matemáticos computacionales”. En él, analiza el papel de las herramientas informáticas en el aprendizaje y en la enseñanza de las matemáticas. Explica nociones como la ejecutabilidad de las representaciones computacionales, la mediación instrumental de las TICs y su transformación en instrumentos matemáticos. http://www.eduteka.org/tema_mes.php?TemaID=0003

[4] Experiencia del Proyecto de Calculadoras en el Departamento del Valle http://eduteka.org/profeinvitad.php?ProfInvID=0003

[5] Ministerio de Educación Nacional de Colombia, “Memorias del Seminario Nacional de Docentes: Uso de Nuevas Tecnologías en el Aula de Matemáticas”, 2002.

En el primer capítulo se presentan los talleres, documentos de trabajo y artículos relevantes que sirvieron de base para la fundamentación técnica, pedagógica y didáctica del uso de la tecnología durante el inicio de la Fase Piloto. En el capítulo dos, se presenta una recopilación de artículos elaborados por el doctor Luis Moreno Armella, que sirvieron para adelantar la discusión académica realizada en los seminarios de fundamentación, asesoría y seguimiento, a lo largo de la fase piloto. En el tercer capítulo se encuentran algunos talleres elaborados por el equipo de educadores matemáticos del Ministerio de Educación con el fin de apoyar el seguimiento y orientar el diseño de actividades de clase. En el cuarto y último capítulo, se presentan los documentos y talleres elaborados por el grupo del Ministerio y por docentes vinculados al proyecto para orientar el curso de profundización en el uso de la tecnología y su impacto pedagógico. http://www.mineducacion.gov.co/documentos/alldocs.asp?it=87&s=1&id=29

CRÉDITOS:

Fragmento del Artículo “Cognición y computación: el caso de la geometría y la visualización”, escrito por Luis Moreno Armella, CINVESTAV-IPN, México; publicado en el capítulo 1 del libro “Memorias del Seminario Nacional de Docentes: Uso de Nuevas Tecnologías en el Aula de Matemáticas”, Ministerio de Educación Nacional de Colombia, 2002. http://www.eduteka.org/pdfdir/MENTechMath1B.php
http://www.mineducacion.gov.co/documentos/alldocs.asp?it=87&s=1&id=29
Permiso de publicación en EDUTEKA concedido por el autor y por el Ministerio de Educación Nacional de Colombia http://www.mineducacion.gov.co

Publicación de este documento en EDUTEKA: Diciembre 13 de 2003.
Última modificación de este documento: Diciembre 13 de 2003.