
Instrumentos Matemáticos Computacionales.
https://eduteka.icesi.edu.co/articulos/Tema3
Instrumentos matemáticos computacionales
Por: Luis Moreno Armella
Luis Moreno Armella, investigador del Departamento de Matemática Educativa del Centro de Investigación y Estudios Avanzados de México-Cinvestav, analiza el papel de las herramientas informáticas en el aprendizaje y en la enseñanza de las matemáticas. Explica nociones como la ejecutabilidad de las representaciones computacionales, la mediación instrumental de las TIC y su transformación en instrumentos matemáticos. Moreno Armella es asesor del proyecto de calculadoras del MEN.
Introducción
Cuando examinamos los textos clásicos de las matemáticas griegas, nos resultan tan familiares que por ello no nos sorprende la expresión de Littlewood quien se refería a los matemáticos griegos como “fellows” de otra universidad, estableciendo así una comparación con los matemáticos de Cambridge.
El rasgo metodológico principal de esos textos es la demostración. La coronación de esa concepción matemática está constituída por Los Elementos de Euclides. Ha sido tal el éxito de esta manera de concebir la disciplina, que solemos olvidar las tensiones que surgieron en el interior de la comunidad matemática en diferentes momentos históricos. Por ejemplo, Arquímedes, –considerado como el mayor de los matemáticos griegos– formuló su punto de vista en los siguientes términos:
En este texto Arquímedes reconoce las bondades de un equilibrio entre la demostración y los experimentos matemáticos que nos permiten reconocer hechos matemáticos.
Refiriéndose al método mecánico, en su Vida de Marcelo, Plutarco comenta que Platón reaccionó con indignación al conocer el de Eudoxio (precursor del método mecánico de Arquímedes) porque representaba “una corrupción de la geometría” (Peitgen et al. 1992). En efecto, en lugar de razonar a partir de los objetos inmateriales, productos del intelecto puro, (i.e.: de los objetos conceptuales de las matemáticas) se apoyaba en objetos materiales y en la percepción sensorial de los mismos.
Me he querido referir a este pluralismo epistemológico de la matemática griega, que puede apreciarse en las posiciones tan divergentes de Arquímedes y de Platón, para establecer una analogía con un tema de actualidad y de la mayor importancia para la educación matemática:
El papel de las herramientas informáticas en el aprendizaje y en la enseñanza de las matemáticas.
Nuestro propósito en este escrito consiste en analizar este problema desde perspectivas que han resultado fructíferas en la investigación actual. La primera de éstas se refiere a la ejecutabilidad de las representaciones computacionales. La segunda, trata aspectos centrales de la mediación instrumental idea tematizada originalmente, desde un punto de vista psicológico, por Vigotski (Kozulin, 1994). Finalmente, trataremos un aspecto importante del trabajo con las herramientas computacionales, a saber, su transformación en instrumentos matemáticos (Rabardel, 1995).
Con relación a estas herramientas, Balacheff & Kaput (1996), han señalado que su mayor impacto es de carácter epistemológico, refiriéndose con ello al hecho que las herramientas computacionales han generado un nuevo realismo matemático. En efecto, los objetos virtuales que aparecen sobre la pantalla se pueden manipular de tal forma que se genera una sensación de existencia casi material. Por ejemplo, podemos trazar una parábola (dibujada por el punto Q) al desplazar el punto P sobre la recta d. Una vez construída la cónica, para quien ha operado el medio ambiente geométrico, la existencia ha dejado de ser virtual: el desarrollo constructivo no ha ocurrido en la imaginación del operador sino sobre la pantalla, aunque siempre, bajo el control de las reglas de la geometría, implícitas en el medio ambiente.
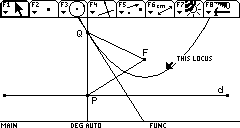
Las herramientas computacionales han modificado profundamente la naturaleza de las exploraciones y la relación de dichas exploraciones con la sistematicidad del pensamiento matemático.
Debido a que los objetos sobre la pantalla son producidos y controlados desde el universo interno de la herramienta computacional ––en términos informales podemos decir que el universo interno equivale a la matemática instalada en el procesador central de la calculadora––, podremos afirmar que estos objetos sobre la pantalla son modelos manipulables de objetos matemáticos.
Estos modelos contribuyen a una mayor interrelación entre la exploración y la sistematicidad ya que ofrecen mayor capacidad de cálculo, mayor poder expresivo y flexibilidad en la transferencia entre sistemas de representación. Además, la exploración respeta explícitamente las reglas sintácticas del medio ambiente. Los sistemas de representación permiten instalar aspectos de nuestro pensamiento en un medio estable, y ejecutable––en el caso de las computadoras. Estos medios llegan a ser parte integral de nuestros recursos intelectuales y expresivos. Permiten, además, generar una forma de realidad virtual asociada a los objetos conceptuales de las matemáticas, y traerlos, virtualizados ya, a la pantalla en donde podemos manipularlos con amplitud.
La mediación instrumental
En la introducción a su libro Oralidad y Escritura, W. Ong (1999, p.11) afirma:
También te podría interesar
UNESCO: Recursos para Nociones Básicas de las TIC
Ver artículoLos computadores como herramienta para potenciar la mente
Ver artículoLa Integración de las TIC en Matemáticas
Ver artículoUNESCO: Recursos para Nociones Básicas de las TIC
Ver artículo- Muchas de las características que hemos dado por sentadas en el pensamiento dentro de la ciencia ... se originaron debido a los recursos que la tecnología de la escritura pone a disposición de la conciencia humana.
La afirmación de Ong es de la mayor importancia. Toca un punto muy sensible con relación a las estructuras cognitivas, a saber, la influencia que tienen los instrumentos de mediación en la arquitectura de la mente humana. Por ejemplo, la escritura ha sido responsable de cambios profundos en la organización funcional de la memoria. Contar con un campo externo, como son los registros escritos, cambia eventualmente las funciones de la memoria biológica. Los registros externos se tornan elementos de reflexión por parte de quien los produce, pero también son sujeto de crítica por parte de otros. De esta manera, la escritura funciona como un mecanismo de socialización del conocimiento. Estos rasgos que en un comienzo son explícitos, con el paso del tiempo ganan en naturalidad y terminan volviéndose invisibles para las generaciones posteriores para las que aquellos medios son parte de su entorno. Esto explica el rasgo de invisibilidad compartido por todas las tecnologías. De manera que, en determinado momento histórico, una tecnología puede tener un impacto decisivo sobre la naturaleza de una disciplina y sobre los mecanismos cognitivos de la sociedad, sin que tales efectos sean posteriormente reconocidos como producto de esa tecnología. Por ejemplo, se puede llegar a creer que existe una actividad matemática pura, al margen de los sistemas matemáticos de representación. Es decir, al margen de la tecnología de la escritura.
De cara a los fenómenos de la invisibilidad, digamos que no hay actividad cognitiva al margen de la mediación instrumental. Ejemplos que sustancien tal afirmación, pueden traerse de diversos campos disciplinarios. Pensemos en un instrumento musical, un piano, digamos. El pianista ha necesitado de un esfuerzo intenso y prolongado para aprender a tocar ese instrumento. Su conocimiento no es independiente del instrumento. Uno no va a escuchar cantar al pianista: va a escucharlo tocar el piano, y a valorar en términos estéticos la naturaleza simbiótica de la relación pianista-piano.
En el desarrollo de las ciencias, digamos la astronomía, por ejemplo, no podemos separar la construcción de los cuerpos conceptuales y las diferentes versiones de telescopio que han estado a disposición de los astrónomos. La simbiosis entre el conocimiento generado y los instrumentos es total.
Las herramientas, como instrumentos de mediación, han sido desarrolladas en distintos medios culturales y en diversos periodos históricos. Son parte integral de las actividades humanas.
Este enfoque sobre la actividad cognitiva ha recibido una atención creciente en los últimos años debido, en parte, a la presencia de las herramientas computacionales en la educación. Allí es necesario entenderlos como herramientas de mediación de las actividades cognitivas orientadas al aprendizaje.
Representaciones ejecutables
Veamos otro ejemplo para sustanciar las observaciones sobre ejecutabilidad de las representaciones que hemos desarrollado líneas arriba. Consideremos la suma (parcial) de la serie armónica:
![]()
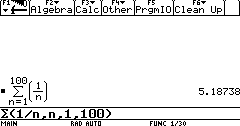
que de acuerdo a la sintaxis de TI-92, se escribe así:
![]()
Una vez introducida la expresión a la calculadora, queda bajo el control del universo interno de la misma. Al pulsar enter, la calculadora efectúa la suma (el resultado aparece a la derecha en la pantalla de la calculadora). Esta acción (realizar la suma) es un acto cognitivo exteriorizado: ya no se realiza en la mente del estudiante o del profesor sino que lo realiza la calculadora:
Un ejemplo más: usar el corrector de ortografía para revisar un texto. Esta es una función que anteriormente estaba reservada a los seres humanos. La máquina no solo registra el pensamiento del escritor sino que procesa la información que queda registrada en ese medio de representación externa. Eso mismo ocurre cuando uno efectúa una operación aritmética con una calculadora, como acabamos de ver, o cuando se usa la agenda electrónica para recuperar un número telefónico.
De modo que al usar una computadora, una persona no sólo tiene a su disposición un espacio de representación externa (como un cuaderno) sino la posibilidad de procesar esa información de cierta manera debido a la ejecutabilidad del sistema de representación que le suministra la máquina.
La mediación instrumental comienza desde el momento en que podemos re-definir los objetos matemáticos en términos de las construcciones ejecutables. No sólo hay representaciones ejecutables sino también construcciones ejecutables––las que se hacen con Cabri, por ejemplo.
De la amplificación a la re-organización conceptual.
Frente a la calculadora, estamos ante dos posibilidades:
i.Entenderla como herramienta de amplificación
ii.Entenderla como herramienta de re-organización cognitiva.
En realidad, como veremos más adelante, estas posibilidades constituyen las dos etapas de un mismo proceso: Es inevitable que al introducir las calculadoras en la actividad de los estudiantes, se termine produciendo una nueva actividad matemática que, a su vez, genere una re-organización del conocimiento de los estudiantes. Debemos apresurarnos a decir que, sin embargo, el paso de (i) a (ii) no es automático y es mas bien lento y complejo. Por esto, tiene sentido desde una perspectiva curricular, examinar a fondo el papel de la calculadora como instrumento de amplificación dentro de un curriculum establecido.
La metáfora de las herramientas de amplificación sugiere pensar en una lupa. La lupa deja ver, amplificado, aquello que podía ser visto a simple vista. No cambia, por esto mismo, la estructura del objeto de nuestra visión. La metáfora de las herramientas de re-organización, sugiere pensar en un microscopio. Con el microscopio podemos ver lo que no era posible sin dicha herramienta. Accedemos entonces a otro nivel de la realidad, cualitativamente distinto. Se abre entonces, la posibilidad de acceder a un conocimiento nuevo.
La re-organización no puede separarse de la amplificación. Son las dos caras de una moneda. A este respecto Dörfler (1993, p. 165) ha señalado que:
Pero si vemos la cognición como un sistema funcional que comprende al individuo y todo su entorno físico y social... se abre la posibilidad de reconocer que las nuevas herramientas tienen un impacto transformador profundo en la cognición…”.
La reflexión en torno a los procesos de amplificación y re-organización también puede darse desde la perspectiva de la transición de herramienta a instrumento matemático que sufren las computadoras y calculadoras (Rabardel, 1995).
De las herramientas a los instrumentos
Por otra parte, es posible que el uso sostenido de la herramienta desemboque en cambios a nivel de las estrategias de solución de problemas, en cambios a nivel de la manera misma como se plantea el problema. En otras palabras, puede ocurrir que el pensamiento matemático del estudiante quede afectado radicalmente por la presencia de la herramienta. Como cuando ya no podemos distinguir entre el pianista y el piano a la hora de la ejecución. El piano “forma parte” del pianista. La herramienta se ha tornado un instrumento. Cuando hablamos de las calculadoras, diremos que la calculadora se ha tornado un instrumento matemático. Es decir, cuando tiene efectos de re-organización conceptual. Cuando la herramienta se torne instrumento, estaremos ante los efectos estructurantes de la herramienta sobre la acción.
Algunos autores se han preocupado por caracterizar el origen de esa transformación. Es decir, se han interesado por la génesis instrumental de las herramientas computacionales (Rabardel, 1995).
En dicha génesis se combinan dos procesos:
i)El sujeto se adapta a la herramienta.
ii)El sujeto adapta la herramienta a sí mismo.
Estos procesos ocurren mediante la producción de esquemas de uso, orientados a las acciones directamente vinculadas a la herramienta. Estas acciones del estudiante están condicionadas por la naturaleza de la herramienta misma.
El uso sostenido de la herramienta estabiliza los esquemas de uso.
Dichos esquemas permiten atribuir un significado a los objetos (matemáticos) en función de la orientación de la actividad y de las tareas a desarrollar. A partir de allí, el empleo de las herramientas (ahora instrumentos) queda controlado por los esquemas.
Referencias
Balacheff,N.&Kaput,J.(1996). Computer-Based Learning Environment in Mathematics. En Bishop, A.J. et al, International Handbook of Mathematical Education, 469-501.
Kozulin, A. (1994). La Psicología de Vygotski. Alianza Editorial, Madrid.
Moreno, L. (2001). Cognición, Mediación y Tecnología. Avance y Perspectiva, vol. 20, pp. 65-68.
Ong, W. (1999). Oralidad y Escritura, Tecnologías de la Palabra. Fondo de Cultura Económica, México.
Peitgen et al. (1992). Fractals for the Classroom, vol. 1 (Introducción de B. Mandelbrot). Springer-Verlag & NCTM.
Rabardel, P. (1995). Les Hommes et les Technologies. Armand Colin, Paris.





