Integrar

Los estudiantes aprenden sobre integrales definidas, mediante límites y sumas de Riemann

Grades 9-12

• Álgebra
  • Representar y analizar situaciones y estructuras matemáticas utilizando símbolos algebraicos. 
• Geometría
  • Utilizar visualización, razonamiento espacial y modelamiento geométrico para resolver problemas
• Medición 
  • Aplicar técnicas apropiadas, herramientas y fórmulas, para determinar medidas. 

• Algebraicos: Los estudiantes deben ser capaces de:
  • trabajar con ecuaciones más complicadas que las ecuaciones polinomiales
• Geometricos:  Los estudiantes deben ser capaces de:
  • graficar ecuaciones algebraicas en el plano coordenado
  • hallar el área de rectángulos y trapecios
• Pre-Calculo:  Los estudiantes deben ser capaces de:
  • entender el concepto de infinito
  • entender y evaluar límites

• Acceso a un navegador
• Lápiz y calculadora
• Copias del material suplementario: 
• Taller de integración

área,promedio,infinito

• Enfoque y repaso

  Haga un repaso de límites, infinito y derivadas como preparación de los estudiantes para esta lección.

  Haga estas preguntas:

  • ¿Qué significa hallar el límite de una función?
  • Frecuentemente una función se aproxima a 0/0 o a 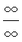 ¿Podemos, en estos casos calcular el límite? ¿Cómo? 
  • ¿Cómo podemos hallar el área bajo una recta tal como  y=x?
  • ¿Cómo se utilizan los limites para calcular la recta tangente a una curva o la derivada de una función
• Objetivos

  Informe a los estudiantes lo que harán y aprenderán con esta lección. Diga algo como esto:

  • Hoy aprenderemos cómo calcular áreas bajo curvas por medio de rectángulos y de trapezoides. Trabajaremos con los computadores, pero no los prendan todavía pues primero quiero mostrarles algo. 

   

• Aportes del maestro

  Pida a los estudiantes calcular el área de un triángulo de base 5 y altura 5. A continuación abra ¡Grafíquelo! y grafique la recta y=x. Haga estas preguntas: 

• ¿Cómo podemos calcular el área entre la gráfica de la función y el eje x, desde 0 hasta 5?
• ¿Podríamos usar la misma clase de triángulo para calcular el área bajo la gráfica de la función y el eje x, desde 0 hasta 10?
• ¿Qué forma tendría el área bajo la recta desde 5 hasta 10?

• Ahora, grafique la curva y = x^2. Pregunte:

• ¿Puede alguien pensar en la forma del área bajo esta curva, desde 0 hasta 5?
• Como lo dijimos anteriormente, el área bajo un segmento de recta es un trapezoide. Dado esto, hay alguna manera de dividir la curva en muchos segmentos para encontrar el área bajo ella? .​
• ¿Podemos calcular el área bajo cualquier línea recta con un trapecio?

• Práctica orientada

  Abra Integrando y cambie los datos a los siguientes:

  • f(x) = x^2
  • Integrar de 0 a 5
  • Número de particiones: 1
  • Método de integración: Trapezoide

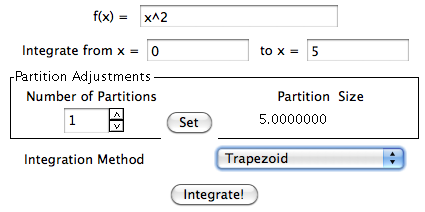
• Formule estas preguntas:

  • ¿Es esta línea recta una muy buena aproximación de y=x^2 de 0 a 5?
  • (Aumenten a tres el número de particiones) ¿Son estas rectas una mejor aproximación de y = x^2 desde  0 hasta 5? Explique su respuesta
  • ¿Qué creen que pasaría si se aumenta el número de particiones a 10 o más?
  • ¿Cómo podríamos calcular el área bajo la curva usando estas rectas?
  • Cuando trabajamos con derivadas dijimos que toda curva se ve como una línea recta en una porción suficientemente pequeña de la curva. En consecuencia, qué pasaría con nuestra aproximación al área bajo la curva a medida que tomamos más y más segmentos cada uno más y  más pequeño?

  Cambie el método de integración a Suma por la izquierda disminuya el número de particiones a 3-5 y pregunte: 

  • Dado que es mucho más fácil calcular el área de los rectángulos que la de los trapecios, ¿podríamos entonces usar más bien rectángulos para calcular el área bajo la curva?
  • (Aumenten a 10 el número de particiones) ¿Pueden, por simple inspección visual establecer la diferencias entre el método de los rectángulos y el de un número igual de particiones en trapecios?
• Práctica independiente

  Haga que los estudiantes trabajen individualmente o en grupos para completar el Taller. Mientras lo hacen, pregúnteles sobre las ventajas de los métodos de suma estudiados.

• Cierre

  Reúna a los estudiantes nuevamente y discuta lo que han aprendido. Pregunte:

  • Visualmente, ¿cuál método piensan ustedes que mejor aproxima el verdadero valor del área bajo la curva? ¿Por qué lo creen así?
  • Con base en los resultados del taller, ¿Cuál creen que es el área bajo sen (x) desde x=0 hasta x= pi? 
  • Por resultados del Cálculo sabemos que el valor exacto de sen(x) desde x=0 hasta x=pi es 2.¿Cuál regla dio un valor más cercano a éste, en 10 particiones?
  • ¿Cómo cambió el error en ambos métodos a medida que se aumentó el número de particiones? ¿Cómo se explica esto?
  • ¿Qué cree usted que pasaría si el número de particiones se incrementara infinitamente? 

Esta lección puede reorganizarse en diferentes formas:

• Si sólo hay un computador disponible, complete el taller con la clase permitiendo que algún estudiante voluntario complete cada sección.
• Si el tiempo lo permite el instructor puede introducir el concepto de integral negativa considerando ecuaciones cuya gráfica queda por debajo del eje x.