Inicio Discusiones Estadística Desviación estándar
Discusiones
Temas
Desviación estándar
Presenta la desviación estándar y describe cómo calcularla.
Estudiante: ¿Puede explicar qué significa desviación estándar? Estoy desarrollando un proyecto para mi clase de biología, tenemos que usar ese concepto y no lo entiendo
Mentor: Seguro. Déjame pensar en un ejemplo que te pudiera ser familiar...espera, tu hermano es un experto tirador del cuerpo de Marines, ¿no es así?
Estudiante: Sip.
Mentor: Okey, ¿Cómo piensas que debe verse un buen blanco de tiro de un tirador experto? ¿Crees que todos los proyectiles disparados impactan exactamente en un mismo punto?
Estudiante: Bueno, ningún tirador es perfecto. Y no se puede sostener un rifle totalmente quieto; se mueve, así sea sólo un poco. En consecuencia los disparos darán cerca unos de otros pero no en el mismo punto.
Mentor: Exactamente. Habrá un poco de lo que llamamos "variación aleatoria". Un disparo puede dar un poco arriba y a la izquierda y otro ligeramente a la derecha, etc. No se puede predecir la siguiente variación, pero si se consideran conjuntamente todas las variaciones, se puede tener una idea de qué tan hábil es el tirador con el rifle, según la variación sea grande o pequeña.
Estudiante: Ok, ya veo.
Mentor: Bien. Ahora podemos enlazar esto con tu pregunta original. Desviación estándar es el nombre dado a una forma de ver qué tan apretados o separados están los datos de un conjunto. Ella permite describir la variación del total de datos de un conjunto, con un solo número. Esto puede ser de utilidad para encontrar qué tan similares son todos los elementos de un conjunto. Por ejemplo, si estuvieras produciendo artículos en una fábrica podrías decir si operarios o las máquinas que elaboran tus productos lo están haciendo bien, es decir, fabricando artículos con poca variación. Si la desviación estándar empieza a aumentar, ello puede indicar que una máquina está experimentando desgaste.
Estudiante: Oh, parece útil. ¿Y con respecto a mi proyecto de biología?
Mentor: Sí, naturalmente. Dime de qué trata el proyecto.
Estudiante: Bueno, yo sembré un puñado de fríjoles y puse a crecer una parte bajo luz incandescente y otra parte bajo luz fluorescente. Pasadas tres semanas medí las longitudes de los tallos y se suponía que debo calcular la longitud media y la desviación estándar de cada grupo. Sé cómo obtener la media. Simplemente, sumo las longitudes y divido la suma entre el número de tallos, pero no entiendo la fórmula para calcular la desviación estándar.
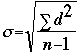
Mentor: Es verdad que luce atemorizante, pero realmente es que hay varios pasos concentrados en una sola expresión. Entonces, como sucede con la mayoría de las expresiones matemáticas complejas, lo mejor es abordar esta de adentro hacia afuera. Empecemos con esa cosa graciosa en zig zag.
Estudiante: Mi profesor nos dijo que es una letra griega, sigma, creo.
Mentor: Sí. Es la letra griega para " S" y la utilizamos con el significado de "suma" o "sumar hasta". En este caso indica sumar los cuadrados de d, en su totalidad.
Estudiante: ¿Y que son los cuadrados de d?
Mentor: Para cada número en tu conjunto de datos, d es la diferencia entre ese número y la media. y d cuadrado es simplemente d multiplicado por sí mismo. Entonces, todo lo que haces es tomar cada número, restarlo de la media y elevar al cuadrado el resultado y después sumarlos todos esos cuadrados.
Estudiante: Entonces eso da cuenta de sigma. ¿El paso siguiente es dividir por n-1?
Mentor: Exactamente, divides la suma de los d al cuadrado por n-1, donde n es el número de datos. Ahora, una vez que has completado eso, ¿qué te dice el signo que contiene al resultado?
Estudiante: ¿Que saque la raíz cuadrada?
Mentor: ¡Correcto! Eso es todo. Entonces, ¿cuál es tu resultado?
